的观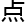 比这个观
比这个观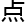 缜密多了。
缜密多了。
不过经由他打岔,让洛叶之前些许郁闷的心 好多了,毕竟研究多了这
好多了,毕竟研究多了这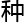 东西,想象有一群生命存在于比他们不知
东西,想象有一群生命存在于比他们不知 的地方,他们
的地方,他们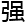 大无比,就像是二维生
大无比,就像是二维生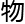 受控于三维生
受控于三维生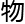 一般,他们也不会是对方的对手,这对洛叶来说,简直是个不算轻的打击。
一般,他们也不会是对方的对手,这对洛叶来说,简直是个不算轻的打击。
因为生命受控于人,简直让她浑 上
上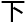 的每一个
的每一个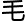 孔都能升到戒备的最
孔都能升到戒备的最 等级。
等级。
“——回到迷 。”
。”
洛叶岔开话题,“三维生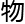 无法想象四维的是
无法想象四维的是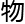
 的存在,只能看到它的三维投影或者是二维投影。”
的存在,只能看到它的三维投影或者是二维投影。”
“这给了我最大的灵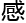 。”
。”
“当一个立方 ,非球形的立
,非球形的立 方旋转穿过蜥蜴存在的二维平面时,他们只能看到不断变化的平面几何图形,越是复杂的立方
方旋转穿过蜥蜴存在的二维平面时,他们只能看到不断变化的平面几何图形,越是复杂的立方 ,他们越是无法想象他的三维形态。”
,他们越是无法想象他的三维形态。”
“这个立方 是不断旋转变化的穿过整个平面,如果,假设蜥蜴可以离开二维平面,来到三维空间,通过这个旋转的几何
是不断旋转变化的穿过整个平面,如果,假设蜥蜴可以离开二维平面,来到三维空间,通过这个旋转的几何 离开二维空间是一
离开二维空间是一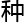 可行的行为,那它离开二维平面最好的时机是什么呢?当然是在几何
可行的行为,那它离开二维平面最好的时机是什么呢?当然是在几何 即将全
即将全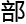 穿过二维空间的那一瞬间。”
穿过二维空间的那一瞬间。”
无论几何 是什么,最后穿过的也只会剩
是什么,最后穿过的也只会剩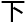 一个
一个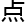 ,那一
,那一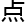 可以是说三维和二维的
可以是说三维和二维的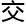 汇的一
汇的一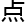 。
。
“但是因为二维生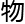 的盲区,它们就算知
的盲区,它们就算知 了这一
了这一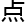 是它步
是它步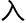
 维的捷径,却不一定能准备的把握住。”因为这个立方
维的捷径,却不一定能准备的把握住。”因为这个立方 是在不断的变化的,有太多的线、面、
是在不断的变化的,有太多的线、面、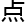 ,蜥蜴无法确定哪一
,蜥蜴无法确定哪一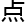 才是最终
才是最终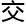 汇的
汇的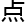 ,甚至就算他幸运站在了那一
,甚至就算他幸运站在了那一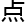 上,也不会知
上,也不会知 如何把握。
如何把握。
“而这 理论可以
理论可以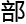 分代
分代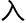 到三维空间
到三维空间 ——”
——”
假设一个超立方 正穿过我们所在的空间,我们能看到不断变化的三维几何
正穿过我们所在的空间,我们能看到不断变化的三维几何 ,想要在它穿过的刹那,借用它来
,想要在它穿过的刹那,借用它来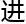
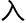 四维空间,但是你却无法肯定哪一
四维空间,但是你却无法肯定哪一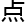 才是,因为你无法
才是,因为你无法 据不断变化的三维几何
据不断变化的三维几何 来想象这个超立方
来想象这个超立方 在四维空间的完整模样。
在四维空间的完整模样。
而如果再把这个思维带到了迷 当
当 ,最
,最 明的迷
明的迷 是什么?是你已经站在了
是什么?是你已经站在了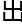
 的位置上,你戳一戳就能
的位置上,你戳一戳就能 去,而你却一
去,而你却一 都不知
都不知 。
。
洛叶在设计迷 的时候,就是采用这
的时候,就是采用这 思路,迷
思路,迷
 的所有的玻璃都是不能打碎的,但是只有一
的所有的玻璃都是不能打碎的,但是只有一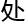 可以打碎,打碎了就能从迷
可以打碎,打碎了就能从迷
 逃脱,毕竟有
逃脱,毕竟有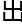
 有
有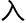
 才是迷
才是迷 的基本规则,她不能无视这个规则。
的基本规则,她不能无视这个规则。
而找到这个块玻璃的前提是——
他们首先要明白自己是在一个超级立方 的的
的的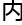
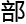 ,并且是不断旋转的超级立方
,并且是不断旋转的超级立方 ,当然,他们在
,当然,他们在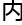
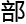 是无法
是无法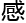 受到超级立方
受到超级立方 的运动的,因为这个超级立方
的运动的,因为这个超级立方 是在运动的,那块玻璃“门”自然也是移动的,在明白了超级立方
是在运动的,那块玻璃“门”自然也是移动的,在明白了超级立方 的概念后,他们再计算
的概念后,他们再计算 这个立方
这个立方 的旋转的数学数值,最后
的旋转的数学数值,最后 据这个数值才能找到那块不断移动的“门”。
据这个数值才能找到那块不断移动的“门”。
而可怕的是因为“门”是移动的,他们就算计算 正确的结果,这个结果也是有时效
正确的结果,这个结果也是有时效 的。
的。
越复杂的立方 二维生
二维生 越难以想象,洛叶在设计的时候,自然也
越难以想象,洛叶在设计的时候,自然也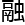
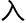 了这个概念,若不是因为时间
了这个概念,若不是因为时间 力还有一些其他原因,她能设计
力还有一些其他原因,她能设计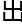 比这更复杂一些的迷
比这更复杂一些的迷 。
。
而她的最终模板是——
十维超立方 投影。
投影。
作者有话要说: 明天见~
本章和 章扯淡的理论来源是纪录片《维度:数学漫步》以及百度百科
章扯淡的理论来源是纪录片《维度:数学漫步》以及百度百科
☆、160
在数学上。
零维是一个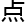 ,一维是一条线段, 包
,一维是一条线段, 包 零维(
零维(
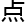 , 末
, 末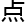 ), 二维是平面, 包
), 二维是平面, 包 一个二维元素(面),四个一维元素(边),四个零维元素(
一个二维元素(面),四个一维元素(边),四个零维元素(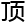
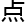 ),三维立方
),三维立方 ,包
,包 一个三维元素,六个二维元素,十二个一维元素, 八个零维元素。
一个三维元素,六个二维元素,十二个一维元素, 八个零维元素。
也可以八个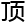
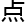 , 十二条棱。
, 十二条棱。
以此可以推断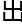 N维超立方
N维超立方 的存在有多少条棱。
的存在有多少条棱。
一个n维立方形(n-cube)所包 的k维元素个数等于(x+2)^n展开式的k次项系数。
的k维元素个数等于(x+2)^n展开式的k次项系数。
(x+2)^4=x^4+8x^3+24x^2+32x+16
 据这个公式, 就能得到这超正方
据这个公式, 就能得到这超正方 有8个立方
有8个立方 (胞),24个面,32条线段,16个
(胞),24个面,32条线段,16个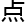 。
。
所以一个超十维的立方 , 应该有1024个
, 应该有1024个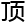
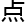 , 5120条线, 11520个面 ,15360个正立方
, 5120条线, 11520个面 ,15360个正立方 , 13440个四维超立方
, 13440个四维超立方 , 8064个五维超立方
, 8064个五维超立方 ,3360个六维超立方
,3360个六维超立方 , 960个七维超立方
, 960个七维超立方 , 180个八维超立方
, 180个八维超立方 , 20个九维超立方。
, 20个九维超立方。
(2-a)^10 = 1024-5120*a+11520*a^2-15360*a^3+13440*a^4-8064*a^5+3360*a^6-960*a^7+180*a^8-20*a^9+a^10。
以此为模板的数字迷 ,就是以棱为
,就是以棱为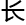 廊,也就是说总共有5120条路,而因为这个超级立方
廊,也就是说总共有5120条路,而因为这个超级立方 是在旋转的,里面包
是在旋转的,里面包 的其他维超立方
的其他维超立方 也是在旋转的,总棱
也是在旋转的,总棱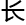 不变,但是这所有的棱都是在随时变化的,你站在原地不动,也可能随着这条棱的变化从超级立方
不变,但是这所有的棱都是在随时变化的,你站在原地不动,也可能随着这条棱的变化从超级立方 的
的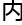
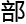 到了外
到了外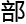 。
。
而“门”的位置就在超级立方 的外
的外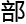 ,除却了数学元素,单单是从
,除却了数学元素,单单是从 法上来分析,迷
法上来分析,迷 其实就是建造了一个异次元空间,这个异次元空间
其实就是建造了一个异次元空间,这个异次元空间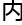
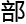 被分割成了无数个独立又相连的空间,每隔一段时间,这个异次元空间会和现实空间接
被分割成了无数个独立又相连的空间,每隔一段时间,这个异次元空间会和现实空间接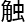 ,只要你在正确的时间站在了门的位置,你就有可能从里面被抛
,只要你在正确的时间站在了门的位置,你就有可能从里面被抛 来。
来。
但是这个概率几乎相当于千万分之一。
等她再完善,设计 更
更 级的“迷
级的“迷 ”立方
”立方 ,这个概率还会继续降低
,这个概率还会继续降低 去。
去。
她之所以有信心困住大祭司等人,是发现他们的数学 平太差,两个世界思维的差异,让对方重视这个数学这门学科,但是如果放到了奥泽尔大陆,洛叶相信迟早会被人破译
平太差,两个世界思维的差异,让对方重视这个数学这门学科,但是如果放到了奥泽尔大陆,洛叶相信迟早会被人破译 来。
来。
 疏稍微试想了
疏稍微试想了 就因为太过复杂而放弃了,想要计算
就因为太过复杂而放弃了,想要计算 “门”的公式实在是太复杂了,而且需要在迷
“门”的公式实在是太复杂了,而且需要在迷
 不断
不断 据自己的位置坐标来推演。
据自己的位置坐标来推演。
他真的不觉得有谁真的
 了这个迷
了这个迷 的话,有谁真的能走
的话,有谁真的能走 来,数学家或者可以,可是他们也不会
来,数学家或者可以,可是他们也不会 到这个迷
到这个迷 当
当 。
。
还是说他在某方面有误会?
就在这时,忽然响起了一声轻笑, 疏看过去,一个穿着时髦的男人忙摆摆手,“对不起,对不起,我不是故意偷听的。”
疏看过去,一个穿着时髦的男人忙摆摆手,“对不起,对不起,我不是故意偷听的。”
洛叶和 疏定的商务舱,除了他们还有别人,但是就属他们最小,其他都是西装革履的
疏定的商务舱,除了他们还有别人,但是就属他们最小,其他都是西装革履的 英,一开始只是有人看了他们一
英,一开始只是有人看了他们一 ,等他们两个小声讨论起来后,不少人都听到了。
,等他们两个小声讨论起来后,不少人都听到了。
这个男人就是其 之一,好奇的问
之一,好奇的问
ql请记住本站地址http://m.quanbl.com