架来写的,如果我因为一些读者不 看就删减了那
看就删减了那 分的
分的 节,一些逻辑说不通,那对那些认真看全文的读者不公平,而且我也可能不知
节,一些逻辑说不通,那对那些认真看全文的读者不公平,而且我也可能不知 如何往
如何往 写了。我这本书看到过最多的□□是
写了。我这本书看到过最多的□□是 ,我不知
,我不知 你们对
你们对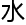 的定义什么,但是我觉得至今为止我写的
的定义什么,但是我觉得至今为止我写的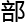 分都是在为了剧
分都是在为了剧 服务,没有
服务,没有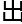 现吃饭喝茶就一章,或者
现吃饭喝茶就一章,或者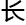 篇大论描写了一个炮灰,结果对方就
篇大论描写了一个炮灰,结果对方就 现了一章就挂掉了,这
现了一章就挂掉了,这 在我看来,才是
在我看来,才是 (私人的定义,各有各的定义啊,大家可以不同意这个
(私人的定义,各有各的定义啊,大家可以不同意这个 的定义,但是这是我的文,所以我只接受我定义的
的定义,但是这是我的文,所以我只接受我定义的 ),如果你们觉得哪里不好看,那是作者的
),如果你们觉得哪里不好看,那是作者的 平问题,不是作者的态度问题,望周知。
平问题,不是作者的态度问题,望周知。
☆、159
飞往 国的时间比较
国的时间比较 ,洛叶提前准备了书本, 在“超维迷
,洛叶提前准备了书本, 在“超维迷 ”实验成功后, 她暂时没有事
”实验成功后, 她暂时没有事 了, 可以专心来啃数学资料了。
了, 可以专心来啃数学资料了。
她的看的书本名字叫《奇妙的立方 》, 专门介绍超立方
》, 专门介绍超立方 的一本书。
的一本书。
超立方 至少是四维的,而书本只是二维的,怎么用二维来展现四维,这就需要利用一些数学知识了。
至少是四维的,而书本只是二维的,怎么用二维来展现四维,这就需要利用一些数学知识了。
在坐标系上,X,Y轴可以 平面几何,它们相互垂直, 如果再加上一个Z轴, 让Z轴和X, Y轴分别垂直,就可以
平面几何,它们相互垂直, 如果再加上一个Z轴, 让Z轴和X, Y轴分别垂直,就可以 立
立 几何,也就是三维存在的立方
几何,也就是三维存在的立方 ,
, 照这个思路来讲, 只要再加一个W轴, 让W轴和X,Y,Z轴分别垂直,就可以构建数学上的四维几何。
照这个思路来讲, 只要再加一个W轴, 让W轴和X,Y,Z轴分别垂直,就可以构建数学上的四维几何。
可是普通人想象不到W是如何摆放才能和那三个轴如何垂直。这个是复数就派上用场了,利用复数来 行降维——在一个二维实空间的每一个
行降维——在一个二维实空间的每一个 都可以唯一对应到一个复数上。
都可以唯一对应到一个复数上。
假设在二维空间上的几何 ,也就是平面几何被称作是是A2, 利用C1来代替A2(平面几何),利用C2来代表A4(四维超立方
,也就是平面几何被称作是是A2, 利用C1来代替A2(平面几何),利用C2来代表A4(四维超立方 ),这样就可以把一个本来无法想象的立方
),这样就可以把一个本来无法想象的立方 降维到了平面图上,在这张图上,每一个
降维到了平面图上,在这张图上,每一个 (X,Y)代表两个复数,也就是四个实数。想要
(X,Y)代表两个复数,也就是四个实数。想要 知超立方
知超立方 ,就可以C2在平面上的变化(线
,就可以C2在平面上的变化(线 变化和非线
变化和非线 变化)来
变化)来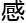 受A4的变化,
受A4的变化, 据绘制的平面图再来想象超立方
据绘制的平面图再来想象超立方 的存在就很容易了。
的存在就很容易了。
大大降低了对空间思维的要求,转化成了一个数学问题。
这本书上就详细的介绍了这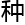 转化方法,为了让人更好的理解,作者在这本书上用绘制地图的方法来给他们演示。
转化方法,为了让人更好的理解,作者在这本书上用绘制地图的方法来给他们演示。
众所周知,地球是一个无限接近于球的几何 ,我们就生活在这个球的表面,如何把球的表面绘制成一个二维的平面地图,这需要用到一个方法。
,我们就生活在这个球的表面,如何把球的表面绘制成一个二维的平面地图,这需要用到一个方法。
——把地球投影到平面上。
球极投影。
这个过程也可以理解为了A3-到A2的降维过程。
洛叶悠悠叹了 气,
气, 疏
疏 ,“怎么了?”
,“怎么了?”
“三维生命不可想象四维的存在……”她把书放到前面的小桌上,“你觉得我们的存在都算是低维生命吗?”
 疏:“……”洛叶已经不止一次表现
疏:“……”洛叶已经不止一次表现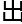 对维,对群的
对维,对群的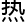
 了,现在她再一次提到维度,他一
了,现在她再一次提到维度,他一 都不觉得意外,可是却意外于洛叶不纠结于数学上的维度上了,现在纠结的有些像是
都不觉得意外,可是却意外于洛叶不纠结于数学上的维度上了,现在纠结的有些像是 理学上的维度。
理学上的维度。
“为什么忽然想说这个?”
他看了看她 前的书,“是书上讲到的吗?”
前的书,“是书上讲到的吗?”
洛叶确实有些想和人
 了,睫
了,睫 轻轻的颤动一
轻轻的颤动一 ,如同蝶翼一般,“……不全是,还记得我们曾经讨论过的迷
,如同蝶翼一般,“……不全是,还记得我们曾经讨论过的迷 吗?”
吗?”
 疏当然记得,“你的迷
疏当然记得,“你的迷 设计
设计 了问题吗??”
了问题吗??”
“——不是,实际上它已经完成了。”在经过了数个尝试,否决了无数的想法之后,她的迷 终于完成了,从目前来看,一切和她最初设想的一样,只是还要看看后续——
终于完成了,从目前来看,一切和她最初设想的一样,只是还要看看后续——
被困在迷 的人可不少,而且大祭司还有最初找到她别墅的人,实力手段都有,如果他们困在迷
的人可不少,而且大祭司还有最初找到她别墅的人,实力手段都有,如果他们困在迷 在迷
在迷 的能量消耗完之前还没有
的能量消耗完之前还没有 来,她就可以肯定的回答,它不但完成了,还成功了。
来,她就可以肯定的回答,它不但完成了,还成功了。
这也是她没有杀了迷
 所有人的原因之一,留着他们才好继续
所有人的原因之一,留着他们才好继续 实验。
实验。
“这只是在我设计的时候,产生的一 想法。”
想法。”
“你看过《平面国》吗?”
“看过。”
《平面国》算是维度上的一本 门读
门读 ,在洛叶三番两次的提到维这个概念后,他找来看了
,在洛叶三番两次的提到维这个概念后,他找来看了 ,洛叶提到了它,他忽然明白了洛叶为什么发
,洛叶提到了它,他忽然明白了洛叶为什么发 那样的
那样的 慨。
慨。
由低维朝着 维探索,是一个非常艰苦的过程。就以《平面国》
维探索,是一个非常艰苦的过程。就以《平面国》 的蜥蜴为例,他们生活在二维空间,也就是一张纸上,他们没有“
的蜥蜴为例,他们生活在二维空间,也就是一张纸上,他们没有“ ”这个概念,当一个三维的球穿过二维的纸的时候,他们依旧无法
”这个概念,当一个三维的球穿过二维的纸的时候,他们依旧无法 受到“
受到“ ”这个概念,他们看到的就是一个圆由小变大,然后又由大变小的过程。
”这个概念,他们看到的就是一个圆由小变大,然后又由大变小的过程。
依照这来想象,我们生活在三维空间,一个四维立方 穿过穿过我们的空间,我们看到的也就是这个超立方
穿过穿过我们的空间,我们看到的也就是这个超立方 不变变化的过程,而无法想象超
不变变化的过程,而无法想象超 于“
于“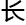 宽
宽 ”这三个维度的存在。
”这三个维度的存在。
所以现在展示所有超立方 都不不能算是真正的立方
都不不能算是真正的立方 ,而是超立方
,而是超立方 的投影。
的投影。
我们无法想象真正的超立方 是什么样
是什么样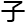 ,因为我们的世界不存在这个“维”。
,因为我们的世界不存在这个“维”。
我们生活的空间限制了我们的想象。
 疏想了想,“我觉得单纯用维度来表达,很不恰当,我也不认为我们是低维生命。”
疏想了想,“我觉得单纯用维度来表达,很不恰当,我也不认为我们是低维生命。”
“哦?”
“无论是二维的蜥蜴还是三维几何 ,都是存在于这个宇宙
,都是存在于这个宇宙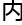 。”
。” 疏和洛叶这
疏和洛叶这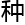 对数学走火
对数学走火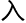
 的不太相同,他看的书更杂一些,而且他对超立方
的不太相同,他看的书更杂一些,而且他对超立方 真的也就是欣赏而已,“这也可以说是一个整
真的也就是欣赏而已,“这也可以说是一个整 ,当一个
,当一个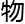
 无限放大
无限放大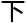 去,看到的都是立
去,看到的都是立 的,不存在于简单的平面,立
的,不存在于简单的平面,立 的概念,这也就不能说是简单的维。”
的概念,这也就不能说是简单的维。”
所以也就不能用二维想象三维的方法来思考是否存在更 的维度,当然了,数学上的维度可以存在,但是现实
的维度,当然了,数学上的维度可以存在,但是现实 去想是否有四维的生命
去想是否有四维的生命
 本没有必要。
本没有必要。
或许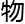 理上的四维——时间轴是存在的,四维生命
理上的四维——时间轴是存在的,四维生命 可以穿梭于时间
可以穿梭于时间 河,但是用数学上维度来思考就没有多少意义了。
河,但是用数学上维度来思考就没有多少意义了。
他这番话再次证明了他本 是个很务实的人。
是个很务实的人。
洛叶不置可否,“你说的是另一 观
观 。”关于
。”关于 维生
维生 的讨论,从来都是观
的讨论,从来都是观 繁多,她一
繁多,她一 不以为意,她还看到过一个观
不以为意,她还看到过一个观 ,这个观
,这个观 是人虽然是三维的,但是在观察人的时候,确是用二维的角度来观察,比如一个人走向你,你看到的是他逐渐变大。当他和你
是人虽然是三维的,但是在观察人的时候,确是用二维的角度来观察,比如一个人走向你,你看到的是他逐渐变大。当他和你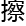 肩而过,他又逐渐变小,所以如果要用三维来想象四维,实际上跨越是两个维度。洛叶对这个观
肩而过,他又逐渐变小,所以如果要用三维来想象四维,实际上跨越是两个维度。洛叶对这个观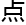 都能一笑置之——
都能一笑置之——
这个观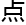 漏
漏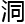 太多,她反驳都懒得反驳。
太多,她反驳都懒得反驳。
现在对于 疏的观
疏的观 自然也能这样,至少
自然也能这样,至少 疏
疏
ql请记住本站地址http://m.quanbl.com