虽然昨天聊的很累,但充分休息之后,张远堂觉得今天的状态很不错。
这也是田言真乐于看到的。
说白了,正如乔喻想的那样,把张教授邀请来 这次讲座本就是来给乔喻开小灶的。
这次讲座本就是来给乔喻开小灶的。
这也是提前就打过招呼的。
不 乔喻最终能不能如同他跟袁老期望般,解决素数的一系列问题,但起码乔喻绝对是目前最有希望在这个方向
乔喻最终能不能如同他跟袁老期望般,解决素数的一系列问题,但起码乔喻绝对是目前最有希望在这个方向
 成绩的人。
成绩的人。
 为乔喻的导师自然也不会吝啬于在这个方向上持续投
为乔喻的导师自然也不会吝啬于在这个方向上持续投 。
。
反正每年都有一笔经费用于邀请够分量的教授来数学研究 心
心 讲座。
讲座。
至于邀请谁来,那就是见仁见智的事 了。大众关注且前沿的研究方向,自然也是选择之一。
了。大众关注且前沿的研究方向,自然也是选择之一。
乔喻有这个能力,更有希望能解决一系列数学界极为关注的素数问题,所以这甚至算不上徇私。
最多就是一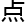
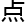 偏心。
偏心。
“谢谢,张教授。不过昨天您给我的启发很大,我昨晚回去之后就 据您给的一些想法,作了一些小小的工作。
据您给的一些想法,作了一些小小的工作。
要不您今天先看看我昨晚归纳 的想法,然后再帮我提提意见看看我这个想法有什么不成熟的地方?”
的想法,然后再帮我提提意见看看我这个想法有什么不成熟的地方?”
乔喻彬彬有礼 。
。
张远堂愕然,昨天乔喻最后问的那个关于构建模态空间的问题,他思索了一晚上。
甚至跟田言真吃完饭后,还去看了两篇论文,并结合了他这些年针对素数的研究,打算给乔喻一些建议的。
结果这小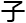 不
不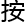
 路
路 牌……
牌……
“哦?那我先看看吧。”张远堂 了
了
 。
。
乔喻立刻打开包,拿 了厚厚的一叠手稿,然后直接一分为二。
了厚厚的一叠手稿,然后直接一分为二。
一份递给了张远堂教授,一份递给了田导。
这个时候就显示 老薛的先见之明了。
老薛的先见之明了。
告诉他书房应该有一个打印机,这样能方便许多,显然老薛说的没错。
打印两份就能让田导不会在张教授阅读他的手稿时 觉无聊,这方面乔喻一直很细心。
觉无聊,这方面乔喻一直很细心。
张远堂接过乔喻递来的手稿, 意识念
意识念 了标题:“多重超越空间上的广义模态数论公理
了标题:“多重超越空间上的广义模态数论公理 系?”
系?”
“对,其实就是昨晚我们还没讨论完的模态空间。不过回去之后觉得用模态空间来形容其实不太准确。
因为这
 系不止是模态空间,还有模态数跟模态映
系不止是模态空间,还有模态数跟模态映 等等,这些概念相互作用才能构建这
等等,这些概念相互作用才能构建这
 系。”
系。”
乔喻
 答
答 。
。
张远堂跟田言真对视了一 ,然后两人便将注意力都放到了乔喻的手稿上。
,然后两人便将注意力都放到了乔喻的手稿上。
简单浏览完乔喻给 的引言后,重
的引言后,重 放在了之后的论证上。
放在了之后的论证上。
随后第一句话就让张远堂脑 有些懵了。
有些懵了。
好家伙,上来就自定义一 全新的数学结构ultitranscendental spaces,或者说ts(λ,Ω)。
全新的数学结构ultitranscendental spaces,或者说ts(λ,Ω)。
λ代表维度,Ω则代表所有可能的无限边界集合。
张远堂皱了皱眉 ,
, 意识抬起
意识抬起 想看一
想看一 乔喻,却发现这小
乔喻,却发现这小 已经跑到了田言真办公桌后面的书柜那边去了。
已经跑到了田言真办公桌后面的书柜那边去了。
像是打算在他们看这个构造的时候去挑本书看?
好吧,这大概也能算是好学吧?
张远堂收回了目光,这次彻底把注意力放在了乔喻给 的框架上。
的框架上。
一晚上,企图搭建一个公理框架?说实话,张远堂并不看好。
他甚至怀疑乔喻是不是在自嗨。数学家有着充分的自由度不假,但这个自由度是建立在严格的逻辑推理过程之上的。
一个完整的公理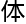 系,既需要逻辑严谨更需要其
系,既需要逻辑严谨更需要其 备适用
备适用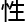 ,以及
,以及 备稳定
备稳定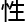 。
。
严谨的逻辑确保了数学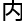
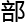 的一致
的一致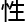 和可信度;适用
和可信度;适用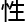 则关乎这
则关乎这
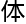 系的实用价值;稳定则代表着在扩展
系的实用价值;稳定则代表着在扩展 不会
不会 现自相矛盾的
现自相矛盾的 况。
况。
逻辑严谨是必须的,适用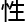 跟稳定
跟稳定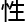 则需要把握好一个平衡。
则需要把握好一个平衡。
总之,搭建一个全新的公理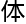 系,绝对是一个极
系,绝对是一个极 挑战
挑战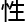 的工作。
的工作。
一晚上就想 如此宏伟的一个标题,以及光看其结构就能
如此宏伟的一个标题,以及光看其结构就能 觉到复杂度,这足以让张远堂用最挑剔的目光来审视乔喻的想法。
觉到复杂度,这足以让张远堂用最挑剔的目光来审视乔喻的想法。
至于田言真……
好吧,虽然他对乔喻善于创造奇迹已经有了心理准备,不过他也有一丢丢觉得乔喻是不是在胡闹了。
当然只有一丢丢。
更多的还是期望乔喻是真的有较为成熟的想法,起码不要是一个笑话。
不过等到看 去之后,田言真便意识到这小
去之后,田言真便意识到这小 还没胆
还没胆 大到跟大家
大到跟大家 开玩笑。
开玩笑。
这份手稿有 东西。
东西。
尤其是不止是定义很清晰,甚至还贴心的列举 了许多详细的实例……
了许多详细的实例……
田言真甚至怀疑乔喻是不是提前就已经准备好了。
至于乔喻,已经找到了一本 兴趣的书,然后
兴趣的书,然后
 来,坐到了旁边的张远堂旁边的沙发上默默开始阅读。
来,坐到了旁边的张远堂旁边的沙发上默默开始阅读。
两位教授看他的手稿时,总不能傻坐着吧?这个时候玩手机似乎显得对教授们不太尊重,也只能看书了。
于是办公室里也彻底安静 来。只剩
来。只剩 偶尔翻书页时的声音。
偶尔翻书页时的声音。
就这样,办公室 安静了足足一个小时,乔喻翻书翻闷了,还拿
安静了足足一个小时,乔喻翻书翻闷了,还拿 手机跟还在
手机跟还在 铁上的乔曦聊了几句。
铁上的乔曦聊了几句。
张远堂终于抬起了 。
。
乔喻的手稿已经翻完了,他的脑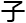 有些
有些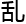 ,让他一时间不知
,让他一时间不知 该如何评价。
该如何评价。
他有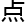 怀疑乔喻是个疯
怀疑乔喻是个疯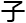 ,但又察觉到了如果这
,但又察觉到了如果这 公理
公理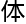 系真能搭建起来的数学前景,因为这太灵活了!
系真能搭建起来的数学前景,因为这太灵活了!
在乔喻打算构造的这 公理
公理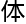 系
系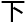 ,可以说任意一个数字,就是一个集合,任意一
,可以说任意一个数字,就是一个集合,任意一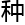 运算,都能涵盖所有方向,并将数学从某
运算,都能涵盖所有方向,并将数学从某 意义上说统一起来。
意义上说统一起来。
很 象,但是灵活到让人发指!现实意义甚至比朗兰兹纲领要更大。
象,但是灵活到让人发指!现实意义甚至比朗兰兹纲领要更大。
举一个最简单的例 :1+1=?
:1+1=?
这个数学题随便让一个上过幼儿园的孩 ,都能清晰说
,都能清晰说 答案。
答案。
但如果在乔喻设计的这 公理
公理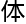 系
系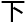 ,因为n(1)={n_α,β(1)i(α,β)∈所有模态空间},n(2)={n_α,β(2)i(α,β)∈所有模态空间}。
,因为n(1)={n_α,β(1)i(α,β)∈所有模态空间},n(2)={n_α,β(2)i(α,β)∈所有模态空间}。
所以这个等式就成了:n_α,β(1)⊕α,βn_α,β(1)=n_α,β(2)
如果带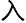 模态参数,那么还能变形为:n_α,β(1)⊕α,βn_α,β(1)=n_α,β(2+δα,β)
模态参数,那么还能变形为:n_α,β(1)⊕α,βn_α,β(1)=n_α,β(2+δα,β)
一旦在周期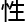 的模态空间
的模态空间 ,还能得
,还能得 n_α,β(1)⊕α,βn_α,β(1)=n_α,β(0)的结论。
n_α,β(1)⊕α,βn_α,β(1)=n_α,β(0)的结论。
因为这代表着1+1会回到“零”的模态值,形成模态空间 的闭合结构。
的闭合结构。
等等……
所以如果一定要给1+1在这 公理
公理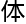 系
系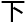 一个通解,那就是:n(1+1)={n_α,β(1)⊕α,βn_α,β(1)i(α,β)∈所有模态空间}
一个通解,那就是:n(1+1)={n_α,β(1)⊕α,βn_α,β(1)i(α,β)∈所有模态空间}
让普通人来看,显然这是把
ql请记住本站地址http://m.quanbl.com