“周教授好。”
“你就是乔喻啊,田先生非常看重你,继续努力。”
“谢谢周教授鼓励。”
“这位是蔡文远教授,主要研究代数几何跟李群的……”
“蔡教授好……”
“楚维华教授,在代数拓扑这块极 的成就……”
的成就……”
随着陈卓 的介绍,会议室里气氛也逐渐熟络起来。说实话,教授们对于乔喻这个孩
的介绍,会议室里气氛也逐渐熟络起来。说实话,教授们对于乔喻这个孩 还
还 陌生,大家无非是看在田言真的面
陌生,大家无非是看在田言真的面 上,来参加这次研讨会。
上,来参加这次研讨会。
至于乔喻的想法更简单,陌生没关系,反正等会大家就都会了解他了。
而且有了陈师兄这个工 人在旁边,很快乔喻就把这次来参加研讨会的教授都认识全了。
人在旁边,很快乔喻就把这次来参加研讨会的教授都认识全了。
移动黑板也在大家寒暄的时候,由工作人员推 了会议室
了会议室 。
。
很快,距离研讨会开始只差三分钟的时候,田言真、罗伯特,跟另一个乔喻没见过的人房间一起走 了会议室。
了会议室。
已经重新坐回自己位置上的乔喻明显 觉到会议室
觉到会议室 气氛突然有些凝滞……
气氛突然有些凝滞……
不是乔喻
 了,主要是大家表现得很明显。
了,主要是大家表现得很明显。
刚刚还在小声讨论着,结果三个人走 来的时候,大家都突然不说话了。
来的时候,大家都突然不说话了。
不至于因为外国友人来了,大家就突然这么守纪律了吧?
乔喻扭 正想跟薛松表达一
正想跟薛松表达一 他的想法,突然发现老薛正盯着刚
他的想法,突然发现老薛正盯着刚 来的三人表
来的三人表 也
也 奇怪的。
奇怪的。
于是小声问 :“薛老师,你咋了?”
:“薛老师,你咋了?”
薛松回过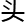 ,面无表
,面无表 的轻声说
的轻声说 :“等会你好好讲,别浪费了田导给你搭的台
:“等会你好好讲,别浪费了田导给你搭的台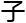 !”
!”
乔喻听懂了这句话的言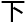 之意,便立刻将目光看向那个他还不认识的人。
之意,便立刻将目光看向那个他还不认识的人。
对他来说很简单的推理。
田导早就明确了会邀请罗伯特教授参加这场研讨会,所以这本就是意料之 的事
的事 ,老薛再次
,老薛再次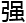 调别浪费了田导搭的台
调别浪费了田导搭的台 ,只能是这个陌生人来
,只能是这个陌生人来 很大了。
很大了。
不过看起来也就是个 瘦严肃的小老
瘦严肃的小老 ,除了有些气场,好像也没什么特别的……
,除了有些气场,好像也没什么特别的……
好在没时间给乔喻胡思 想了,他的导师再次担任起主持人的角
想了,他的导师再次担任起主持人的角 。
。
“非常 谢大家能来参加今天这场研讨会,尤其是
谢大家能来参加今天这场研讨会,尤其是 谢罗伯特教授跟张树文教授能够在百忙之
谢罗伯特教授跟张树文教授能够在百忙之 亲自前来指导我的学生乔喻在数学上的一些奇思妙想。
亲自前来指导我的学生乔喻在数学上的一些奇思妙想。
今天这场研讨会主要讨论的问题是关于利用完备空间、模形式理论与p- 几何等工
几何等工 ,研究代数曲线x上的有理
,研究代数曲线x上的有理 个数上界问题。好了,乔喻你可以开始发言了。”
个数上界问题。好了,乔喻你可以开始发言了。”
说完,田导便坐回到了位置上,乔喻也半 不怯场,立刻站了起来。
不怯场,立刻站了起来。
“谢谢各位老师能来参加这次研讨会,那个,关于我一些不成熟的想法,都已经打印 来,就是大家桌面上放的那叠类似稿纸的东西。
来,就是大家桌面上放的那叠类似稿纸的东西。
对了,还要特别 谢罗伯特教授今天的讲座对我的启发,以及我的导师田言真教授对我的指导。正如刚刚田导说的那样,我在近期阅读了舒尔茨教授跟罗伯特教授的论文之后,突然就有了这么一个很大胆的想法。”
谢罗伯特教授今天的讲座对我的启发,以及我的导师田言真教授对我的指导。正如刚刚田导说的那样,我在近期阅读了舒尔茨教授跟罗伯特教授的论文之后,突然就有了这么一个很大胆的想法。”
乔喻话音刚落,几乎所有人都拿起了桌面上的那份报告,太简陋了,刚刚大家也就提前几分钟来到会议室,忙着寒暄去了,还真没谁拿起来认真看上一 。
。
倒是坐在田言真 边的张树文跟罗伯特教授已经拿起了那本简陋的册
边的张树文跟罗伯特教授已经拿起了那本简陋的册 开始翻看。
开始翻看。
乔喻开场白讲完了之后,已经切 正题。
正题。
“我的想法就是借助彼得·舒尔茨教授搭建的完备空间理论,利用模形式理论、-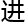 几何和量
几何和量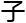 化同调范畴,推导
化同调范畴,推导 代数曲线上有理
代数曲线上有理 的上界表达式。
的上界表达式。
要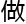 到这一
到这一 ,首先就需要考虑曲线x的几何背景,尤其是其亏格g(x)。亏格是一个重要的拓扑不变量,表示曲线的几何复杂
,首先就需要考虑曲线x的几何背景,尤其是其亏格g(x)。亏格是一个重要的拓扑不变量,表示曲线的几何复杂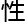 。对于亏格 g≈gt;1的曲线,faltgs定理告诉我们有理
。对于亏格 g≈gt;1的曲线,faltgs定理告诉我们有理 数量是有限的。
数量是有限的。
但这还不够,因为我们都希望得到一个
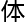 的上界。
的上界。 据几何分析亏格越
据几何分析亏格越 ,代数曲线的复杂
,代数曲线的复杂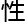 增加,这意味着有理
增加,这意味着有理 的数量相对减少。所以我的初步猜想是:n(x)≤c(g)。
的数量相对减少。所以我的初步猜想是:n(x)≤c(g)。
然后我会从几个设想来论证这个结果,虽然这个结果我认为是没错的,但常数c的
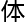 公式,我暂时还无法证明
公式,我暂时还无法证明 来,但我想到了几个很有意思的方法来推导常数c的结果。
来,但我想到了几个很有意思的方法来推导常数c的结果。
只是这些方法还没能证明,所以希望各位老师们能给我些启发。首先,我们引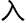 模空间,设x是亏格为g的代数曲线,其模空间g参数化了所有亏格为g的曲线。
模空间,设x是亏格为g的代数曲线,其模空间g参数化了所有亏格为g的曲线。
因为模形式与模空间密切相关,所以我理解为定义在模空间上的某些函数,它们对曲线的复杂度提供几何约束。这样设模形式的等级为k,我们再假定存在一个常数a1,使得:n(x)≤c1(g,k)=a1gkα……”
台 ,会议室
,会议室 所有的教授们都已经收起了之前轻松的心态,神
所有的教授们都已经收起了之前轻松的心态,神 开始变得凝重起来。
开始变得凝重起来。
要说唯一表 没什么变化的,大概就只有田言真跟薛松两人了。
没什么变化的,大概就只有田言真跟薛松两人了。
这一 坐在最后面的陈卓
坐在最后面的陈卓 能作证。
能作证。
他对乔喻讲的 容没什么兴趣,所以将更多的注意力放到了对面导师跟那两位大
容没什么兴趣,所以将更多的注意力放到了对面导师跟那两位大 的表
的表 上。
上。
很明显,田导的心态很放松,只是安静的看着乔喻在板书上书写,他 边的两位大佬,一位眉
边的两位大佬,一位眉 拧成了川字,另一个已经拿起笔开始在文稿旁边写写画画……
拧成了川字,另一个已经拿起笔开始在文稿旁边写写画画……
陈卓
 觉心态有
觉心态有 崩了……
崩了……
不是吧,大家都是认真的啊?所以并不是田导想 推小师弟,这
推小师弟,这 都没被证明的玩意儿大家也能认可?
都没被证明的玩意儿大家也能认可?
是的,陈卓 得知今天
得知今天 午这场研讨会的时候,他是真觉得田导就是想让小师弟跟大家混个脸熟。毕竟田导也说了,乔喻这些都还只是想法……
午这场研讨会的时候,他是真觉得田导就是想让小师弟跟大家混个脸熟。毕竟田导也说了,乔喻这些都还只是想法……
哪有针对想法就这么玩的?陈卓 甚至觉得田导太着急了,毕竟这个小师弟才特么十五岁!虽然能参加o还拿第一,证明
甚至觉得田导太着急了,毕竟这个小师弟才特么十五岁!虽然能参加o还拿第一,证明
 知识肯定是熟练掌握了,但大学知识都不知
知识肯定是熟练掌握了,但大学知识都不知 接
接 过没,他懂个
过没,他懂个 的科研啊!
的科研啊!
他甚至觉得乔喻能看懂彼得·菲尔茨的论文都是在说梦话。但现在光看教授们的表 完全不是这么回事,因为能看
完全不是这么回事,因为能看 大家是真的都开始思考了……
大家是真的都开始思考了……
这特么的,小师弟是真要逆天了?
更让他绝望的是,台上的乔喻不但没有半 怯场,还越讲越兴奋,因为许多教授已经开始认真看他的板书,等等,那位罗伯特教授甚至拿
怯场,还越讲越兴奋,因为许多教授已经开始认真看他的板书,等等,那位罗伯特教授甚至拿 了手机拍
了手机拍 他板书的
他板书的 容……
容……
“……到这一步我们可以引 -
- 数域与舒尔茨教授的同调理论,我们知
数域与舒尔茨教授的同调理论,我们知 对于每个质数p,etale同调群的
对于每个质数p,etale同调群的 质可以约束曲线上有理
质可以约束曲线上有理 的局
的局 分布。
分布。
那么 据舒尔茨的-
据舒尔茨的- hod理论,就可以推导
hod理论,就可以推导 以
以 不等式:n(x)≤c2(g,p)=a2g2log(p)。这里有个
不等式:n(x)≤c2(g,p)=a2g2log(p)。这里有个 很重要,舒尔茨的-
很重要,舒尔茨的- hod理论的一个
hod理论的一个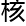 心特
心特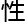 是其
是其 备完备
备完备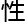 。
。
所以如果我们推导的不等式成立,就可以从曲线在局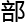 域的
域的 质
质 发,推导
发,推导 全局上的几何约束,所以我们需要证
全局上的几何约束,所以我们需要证
ql请记住本站地址http://m.quanbl.com