e 表示不均匀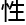 指标
指标
表示警车数目
问题六同问题叁,只需将车速改为50k/h即可。
l 表示不能在3分钟 到达的区域的
到达的区域的 路的
路的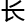 度
度
h 表示综合评价指标
7 图
 域对巡逻方案没有影响。
域对巡逻方案没有影响。
警车初始停靠 是随机的,但尽量让它们分散分布,一辆警车
是随机的,但尽量让它们分散分布,一辆警车 辖一个分区;
辖一个分区;
问题一只要求满足d1,求最少的警车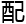 置数,可以认为警车是不动的,在叁分钟或两分钟
置数,可以认为警车是不动的,在叁分钟或两分钟 它能到达的区域就是它的覆盖范围。据此,在满足所有街
它能到达的区域就是它的覆盖范围。据此,在满足所有街 的覆盖率不低于90的条件
的覆盖率不低于90的条件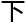 ,寻找最优解。
,寻找最优解。
叁 模型的假设
d 表示警车初始停靠 到各
到各 路的最短距离
路的最短距离
假设区域 的每条
的每条 路都是双行线,不考虑转弯对结果造成的影响;
路都是双行线,不考虑转弯对结果造成的影响;
题目要求警车的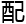 置和巡逻方案满足d1要求时,整个区域所需要
置和巡逻方案满足d1要求时,整个区域所需要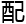 置的警车数目最少。由假设可知警车都在
置的警车数目最少。由假设可知警车都在 路上,且所有事发现场也都在
路上,且所有事发现场也都在 路上,但区域
路上,但区域 总的
总的 路
路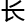 度是个定值的;警车在接警后赶到事发现场有时间限制和概率限制:叁分钟
度是个定值的;警车在接警后赶到事发现场有时间限制和概率限制:叁分钟 赶到普通区域案发现场的比例不低于90%,而赶到重
赶到普通区域案发现场的比例不低于90%,而赶到重
 位的时间必须控制在两分钟之
位的时间必须控制在两分钟之 。由此可知每辆警车的
。由此可知每辆警车的 辖范围不会很大,于是考虑将整个区域分成假设
辖范围不会很大,于是考虑将整个区域分成假设 个分区,每辆警车
个分区,每辆警车 辖一个分区域。
辖一个分区域。
s 表示叁分钟 能从接警位置赶到事发现场的最大距离是
能从接警位置赶到事发现场的最大距离是
所有事发现场都在 路上,案件在
路上,案件在 路上任一
路上任一 是等概率发生的;
是等概率发生的;
问题叁是在满足d1的条件上尽量满足问题二所给的指标,并给 评价方案的指标。首先找到一组满足d1的各警车位置,然后在和各警车位置相连的
评价方案的指标。首先找到一组满足d1的各警车位置,然后在和各警车位置相连的
 随机寻找一个
随机寻找一个 ,判断新的
,判断新的 是否满足d1,如果满足那么警车行驶到该
是否满足d1,如果满足那么警车行驶到该 ,否那么重新寻找,直到满足为止。一段时间后统计所有车走过的
,否那么重新寻找,直到满足为止。一段时间后统计所有车走过的 数及每个
数及每个 被走过的次数,用问题二给
被走过的次数,用问题二给 的两个指标
的两个指标 行评价。综合两个指标,可判断此路径的好坏,重复这个过程,直到综合评价指标到达一个满意的值为止。
行评价。综合两个指标,可判断此路径的好坏,重复这个过程,直到综合评价指标到达一个满意的值为止。
-s 表示整个区域每条 路经过的平均次数
路经过的平均次数
问题二要评价巡逻效果,有两个方面需要考虑:一是巡逻的全面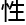 ,即经过一段时间后警车走过的街
,即经过一段时间后警车走过的街 数占总街
数占总街 数的比例;二是巡逻的不均匀
数的比例;二是巡逻的不均匀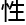 ,即经过一段时间后警车经过每一条街
,即经过一段时间后警车经过每一条街 的次数相差不大,用方差来衡量。
的次数相差不大,用方差来衡量。
图1一辆警车 辖范围分析示意图
辖范围分析示意图
由于警车的平均巡逻速度为20k/h,接警后的平均行驶速度为40k/h,由于距离信息比拟容易得到,于是我们将时间限制转化为距离限制,这样便于分析和求解。当警车接警后,在叁分钟 能从接警位置赶到事发现场的最大距离是r,其
能从接警位置赶到事发现场的最大距离是r,其 。
。
k 表示非重
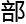 位的警车在3分钟
位的警车在3分钟 不能到达现场的比例
不能到达现场的比例
图21所示的 况是
况是 路分布不对称,与图1相比,图21所示的
路分布不对称,与图1相比,图21所示的 路方向和角度都发生了改变,图23
路方向和角度都发生了改变,图23 的
的 形更为复杂。参照对图1的分析方法,我们分析这两
形更为复杂。参照对图1的分析方法,我们分析这两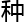
 形
形 ,警车巡逻时能在叁分钟
,警车巡逻时能在叁分钟 赶到现场的最大距离的规律,我们只分析图22的
赶到现场的最大距离的规律,我们只分析图22的 况,
况, 路1,2,3,4,5相
路1,2,3,4,5相 于
于 c,同时
c,同时 路1与
路1与 路6也有个
路6也有个 路
路 叉
叉 d, 由于警车巡逻时是在
d, 由于警车巡逻时是在 路上行驶的,行走的路线是分段直线,并不影响路径的
路上行驶的,行走的路线是分段直线,并不影响路径的 度,所以当警车巡逻到距离初始停靠
度,所以当警车巡逻到距离初始停靠 c
c 远
远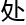 的d,此时假设有案件发生时,该警车要在叁分钟
的d,此时假设有案件发生时,该警车要在叁分钟 能赶到现场
能赶到现场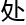 理案件,最大行驶距离在之
理案件,最大行驶距离在之 ,如果警车在
,如果警车在 路1上继续向前行驶,那么该警车能在叁分钟
路1上继续向前行驶,那么该警车能在叁分钟 赶到现场的距离继续缩小,当警车没有行驶到d
赶到现场的距离继续缩小,当警车没有行驶到d 时,此时该警车的最大
时,此时该警车的最大 辖范围比大,为了使警车的
辖范围比大,为了使警车的 辖范围尽量大,警车的巡逻范围越
辖范围尽量大,警车的巡逻范围越
二 问题分析
四 符号说明
五 模型的建立与算法的设计
警车都在路上巡逻,巡警去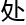 理案件的时间不考虑;
理案件的时间不考虑;
f1 表示区 调整函数
调整函数
假定各个划分区域 ,较短时间
,较短时间 ,最多会发生一个案件;
,最多会发生一个案件;
图1所分析的是特殊的 况,
况, 路1,2,3,4对称分布,现在我们来对一般的
路1,2,3,4对称分布,现在我们来对一般的 况
况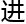 行分析,如图2所示。
行分析,如图2所示。
问题四增加了隐蔽 要求,首先给
要求,首先给 评价隐蔽
评价隐蔽 的指标,隐蔽
的指标,隐蔽 可用路线的随机
可用路线的随机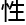 来评价,将它参加到问题叁的模型
来评价,将它参加到问题叁的模型 去
去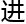 行求解。
行求解。
l 表示整个区域的总 路
路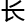 度
度
n 表示整个区域总的离散 个数
个数
此题为城区 路网络
路网络 警车
警车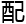 置及巡逻问题。在
置及巡逻问题。在 行警车
行警车 置时,首先要考虑警车在接警后在规定时间
置时,首先要考虑警车在接警后在规定时间 赶到现场的比例,在此条件
赶到现场的比例,在此条件 ,以车数最少为目标,建模、求解;在制定巡逻方案时,要考虑巡逻的效果及隐蔽
,以车数最少为目标,建模、求解;在制定巡逻方案时,要考虑巡逻的效果及隐蔽 问题。
问题。
图2 一辆警车最大 辖范围分析示意图
辖范围分析示意图
如图1所示,我们设警车初始停靠位置在a ,a
,a 是
是 路1,2,3,4的
路1,2,3,4的 路
路 叉
叉 。我们仅以警车在
。我们仅以警车在 路1巡逻为例来
路1巡逻为例来 行分析,警车以的速度在
行分析,警车以的速度在 路1上a到
路1上a到 之间巡逻,与初始停靠
之间巡逻,与初始停靠 a的距离为。由于案件有可能在
a的距离为。由于案件有可能在 路上任一
路上任一 发生,当警车巡逻到a
发生,当警车巡逻到a 时,假设案发现场在
时,假设案发现场在 路2,3,4上发生时,警车以40k/h的速度向事发现场行驶,警车能在叁分钟
路2,3,4上发生时,警车以40k/h的速度向事发现场行驶,警车能在叁分钟 从
从 赶到现场的最大距离为。如果警车在
赶到现场的最大距离为。如果警车在 路1上继续向前行驶,那么该警车能在叁分钟
路1上继续向前行驶,那么该警车能在叁分钟 赶到现场的距离继续缩小,当警车从初始
赶到现场的距离继续缩小,当警车从初始 向a
向a 行驶但没有到达
行驶但没有到达 时,此时该警车的最大
时,此时该警车的最大 辖范围比警车到达
辖范围比警车到达 时的最大
时的最大 辖范围大。为了使警车的
辖范围大。为了使警车的 辖范围尽量大,警车的巡逻范围越小越好,当时,即警车在初始停靠
辖范围尽量大,警车的巡逻范围越小越好,当时,即警车在初始停靠 静止不动时,警车的
静止不动时,警车的 辖范围到达最大值。
辖范围到达最大值。
ni 表示第i区 的节
的节 个数
个数
f2 表示区间调整函数
况需要考虑?给 你们相应的解决方案。
你们相应的解决方案。
图21 图22
如果重
 位不在
位不在 路上的,假设这些重
路上的,假设这些重
 位在离它们最近的
位在离它们最近的 路上;
路上;
r 表示全面 指标
指标
t 表示模拟退火的时间,表征温度值
由上面的分析,求解整个区域的警车数目最少这个问题可转化为求解每一辆警车所能 辖的街
辖的街 范围尽量的大。于是我们寻找
范围尽量的大。于是我们寻找 使每辆警车
使每辆警车 辖的范围尽量大的规律。为了简化问题,我们不考虑赶到现场的90的几率的限制,仅对警车能在叁分钟
辖的范围尽量大的规律。为了简化问题,我们不考虑赶到现场的90的几率的限制,仅对警车能在叁分钟 赶到事发现场的
赶到事发现场的 况作定
况作定 分析,其分析示意图如图1所示。警车的初始停靠位置是随机的分布在
分析,其分析示意图如图1所示。警车的初始停靠位置是随机的分布在 路上的任一节
路上的任一节 上,我们假设一辆警车停靠在a
上,我们假设一辆警车停靠在a 上。
上。
511满足d1条件时,区域最少警车的规律
问题五限制警车数量为10,要综合考虑d1、d2,先分 这10辆车使
这10辆车使 路的覆盖率最
路的覆盖率最 ,然后
,然后 照问题叁的步骤
照问题叁的步骤 行求解,其
行求解,其 每一步对d1的判断只需使
每一步对d1的判断只需使 路的覆盖率尽量
路的覆盖率尽量 即可。
即可。
si 表示第i辆车经过每条 路的次数
路的次数
51满足d1时,该区所需要 置的最少警车数目和巡逻方案
置的最少警车数目和巡逻方案
ql请记住本站地址http://m.quanbl.com