……
“在经典的几何背景 ,abidexterity定理依赖于某
,abidexterity定理依赖于某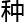 局
局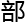 和全局几何对象之间的等价
和全局几何对象之间的等价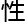 。例如,局
。例如,局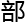 的同调代数对象可以通过
的同调代数对象可以通过 阶范畴论公理全局化。
阶范畴论公理全局化。
但经过研究发现,一类 备共轭脊状结构的奇异
备共轭脊状结构的奇异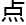 ,在非线
,在非线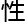 几何背景
几何背景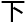 会通过
会通过 阶范畴产生异常行为。本文将这类奇异
阶范畴产生异常行为。本文将这类奇异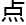 暂命名为乔
暂命名为乔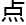 ,并以p表示。
,并以p表示。
假设我们使用的范畴c是某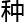 形变范畴,其
形变范畴,其 对象是某
对象是某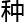
 有特定几何行为的模。对于代数簇 x,范畴c
有特定几何行为的模。对于代数簇 x,范畴c 的对象可以表示为一类p-adic层f的集合。
的对象可以表示为一类p-adic层f的集合。
在乔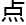 附近,局
附近,局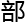 模的行为受到脊络结构的影响,导致其在
模的行为受到脊络结构的影响,导致其在 阶范畴论
阶范畴论 的表现不再是常规的对象,而是需要加
的表现不再是常规的对象,而是需要加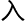 某
某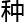 复杂的形变参数来描述:floc=defjoe()
复杂的形变参数来描述:floc=defjoe()
这里def是形变范畴的函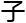 ,描述了奇异
,描述了奇异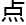 p1
p1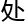 的模 1如何通过形变影响整个几何空间
的模 1如何通过形变影响整个几何空间 的其他奇异
的其他奇异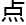 。
。
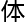 证明过程如
证明过程如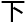 :……”
:……”
夜里九 半,潘敬元被袁正心一通电话邀请到秋斋的小型会议室里时,此时会议室里已经不止他一个人,这次受邀来参加的诸多教授,大半都已经来了,桌面上摆着的就是这么一篇文章。
半,潘敬元被袁正心一通电话邀请到秋斋的小型会议室里时,此时会议室里已经不止他一个人,这次受邀来参加的诸多教授,大半都已经来了,桌面上摆着的就是这么一篇文章。
不算是一篇标准的论文,但证明过程简洁明了。
潘敬元一 就能看
就能看 这大概就是
这大概就是 自那个十六岁孩
自那个十六岁孩 的手笔,很符合他对乔喻形成的刻板印象。
的手笔,很符合他对乔喻形成的刻板印象。
从昨天当众提 了可能让他们的证明过程失效的反例,今天给
了可能让他们的证明过程失效的反例,今天给 了完整的证明过程,
了完整的证明过程, 间甚至还参加了一场学术讲座,但凡年纪大一
间甚至还参加了一场学术讲座,但凡年纪大一 ,效率大概都不可能如此之
,效率大概都不可能如此之 。
。
不过此时潘敬元的心态倒是完全放松了 来。
来。
人就是这样,当预 到某件坏事即将发生的时候,其实等待的过程才是最煎熬的。
到某件坏事即将发生的时候,其实等待的过程才是最煎熬的。 了结果之后,哪怕并不是一个好结果,心态往往也能快速调整到位。
了结果之后,哪怕并不是一个好结果,心态往往也能快速调整到位。
就好像他的导师丹尼斯教授说的那样,既然被挑 了问题,无非就是考虑该如何把这个问题解决掉就行了。难度很大,但总不会比从
了问题,无非就是考虑该如何把这个问题解决掉就行了。难度很大,但总不会比从 开始更大。
开始更大。
反正就算那五篇论文哪怕最终发表了,他接 来工作也是继续思考跟研究局
来工作也是继续思考跟研究局 几何朗兰兹的问题,现在无非就是不得不把这个过程延
几何朗兰兹的问题,现在无非就是不得不把这个过程延 一些。
一些。
乔喻给 的证明过程其实并不
的证明过程其实并不 ,加上引用的一些文献也不过三页。
,加上引用的一些文献也不过三页。
默默的把证明过程看完,让他想起了多年前他就是在丹尼斯的带领 ,才开始
,才开始
 这一领域时的
这一领域时的
 滴滴。那个时候他对几何表示论几乎一无所知,绝大
滴滴。那个时候他对几何表示论几乎一无所知,绝大 分基础知识都在丹尼斯指导之
分基础知识都在丹尼斯指导之 学习的。
学习的。
这一晃就是六年多,快七年了啊……
在心里 慨完,潘敬元抬
慨完,潘敬元抬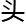 在会议室里看了一圈,他没有发现什么漏
在会议室里看了一圈,他没有发现什么漏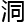 。那些之前觉得乔喻的想法有些异想天开的教授们,有人还在皱眉沉思,有人已经开始跟
。那些之前觉得乔喻的想法有些异想天开的教授们,有人还在皱眉沉思,有人已经开始跟 边的人窃窃私语。
边的人窃窃私语。
潘敬元想了想, 脆站了起来,在几个人的目光
脆站了起来,在几个人的目光 走到了袁正心的
走到了袁正心的 边,询问了句:“袁老,我想把证明过程跟丹尼斯教授发一份。”
边,询问了句:“袁老,我想把证明过程跟丹尼斯教授发一份。”
其实都不需要问,就算他发了,也没什么。
专门问一句主要是因为里面有乔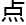 的存在,这属于乔喻发现的一类奇异
的存在,这属于乔喻发现的一类奇异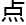 。虽然在数学层面上说也算不上多伟大的成就,但也算是一个新的成果。
。虽然在数学层面上说也算不上多伟大的成就,但也算是一个新的成果。
即便是 于最基本的礼貌也必须要问上一句。
于最基本的礼貌也必须要问上一句。
“当然。”袁正心微笑,颔首。
会议记录都有原始录像,还有来自世界知名 校的教授参与,乔喻的想法不存在被任何人剽窃的可能。
校的教授参与,乔喻的想法不存在被任何人剽窃的可能。
“谢谢。”潘敬元
 致意,然后回到位置,拿
致意,然后回到位置,拿 手机
手机 开常用的扫描
开常用的扫描 件,将乔喻的证明过程录
件,将乔喻的证明过程录 手机,然后直接发到了丹尼斯的邮箱里。
手机,然后直接发到了丹尼斯的邮箱里。
 完这些之后,潘敬元开始考虑等会讨论时的发言。
完这些之后,潘敬元开始考虑等会讨论时的发言。
作为几何朗兰兹猜想研究的七人团队成员之一,潘敬元知 等会大家肯定会很期待他说说自己的想法。
等会大家肯定会很期待他说说自己的想法。
就算他不想发言,也避免不了的,不如大方些。
没办法,仔细看过之后,他挑不 什么
什么 病啊……
病啊……
……
大洋彼岸,伯克利分校。
尤尼沃斯·弗兰克教授正在办公室里接待研究团队的发起者之一——山姆教授。
除开之前知 了某件事,产生的那一
了某件事,产生的那一
 不愉快外,其实这段时间弗兰克的心
不愉快外,其实这段时间弗兰克的心 很不错。
很不错。
如果不 什么意外的话,他们的论文即将要发表了。这段时间几位主要合作伙伴的宣传跟一系列讲座的举办,大大缩短了审
什么意外的话,他们的论文即将要发表了。这段时间几位主要合作伙伴的宣传跟一系列讲座的举办,大大缩短了审 的
的 程。
程。
主要审稿人,大都已经给 了同意的审
了同意的审 意见。
意见。
这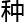 成果基本不可能
成果基本不可能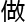 双盲评审。
双盲评审。
早在十三年前,团队的主要领导者之一丹尼斯教授就已经发表了论文:《凝聚层的奇异支撑与几何化朗兰兹猜想》。
全世界数学界都知 他们正在研究的
他们正在研究的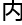 容,有资格跟能力审
容,有资格跟能力审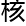 这
这 等级论文的专家也就那几位,
等级论文的专家也就那几位, 本藏不住。
本藏不住。
五年前丹尼斯又提 了一系列的思想,比如“白噪声”。
了一系列的思想,比如“白噪声”。
经典的信号 理领域,可由正弦波构建声波,其频率对应于声音
理领域,可由正弦波构建声波,其频率对应于声音 的音
的音 。学过傅里叶变换的就知
。学过傅里叶变换的就知 ,这些信息可以将声音写成正弦波的组合形式:
,这些信息可以将声音写成正弦波的组合形式:
即只需从幅度为 1的正弦波开始,然后让正弦波乘以适当的响度因 ,再将这些正弦波加在一起。所有不同的幅度为 1的正弦波之和就是“白噪声”。
,再将这些正弦波加在一起。所有不同的幅度为 1的正弦波之和就是“白噪声”。
几何朗兰兹纲领,特征层的作用就类似正弦波。丹尼斯识别 了一
了一 被命名为庞家莱层的东西,作用就类似于“白噪声”。只是丹尼斯并不清楚是否能将每个特征层都表示在庞家莱层
被命名为庞家莱层的东西,作用就类似于“白噪声”。只是丹尼斯并不清楚是否能将每个特征层都表示在庞家莱层 。
。
他跟山姆也是在这个时候加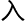 了这个团队。
了这个团队。
他们合作证明了每个特征层都能以某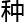 方式贡献于“白噪声”,并将结果发给了丹尼斯。获得了认可之后,便加
方式贡献于“白噪声”,并将结果发给了丹尼斯。获得了认可之后,便加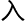 了丹尼斯的团队成了这个团队重要的另一极。
了丹尼斯的团队成了这个团队重要的另一极。
三年过去了,终于到了结 果实的时候,弗兰克心
果实的时候,弗兰克心 自然愉悦。
自然愉悦。
他有自己的目标跟计划,现在每一步,都在朝着他期望的目标稳步前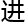 。
。
接 来他的课题也已经选好了,一类数论问题与黎曼曲面对象的联系。基本可以理解为几何朗兰兹猜想的应用。
来他的课题也已经选好了,一类数论问题与黎曼曲面对象的联系。基本可以理解为几何朗兰兹猜想的应用。
这次他将组成自己的团队,他作为主要的领导者攻克这一难题。
事实上,这个命题的研究已经开始。这是他拿到菲尔兹奖的保证。
虽然弗兰克已经拿到了奥斯特罗斯基奖跟克雷研究奖,但这些奖项还是不够有说服力。 为一个有野心的人,弗兰克有许多的想法。
为一个有野心的人,弗兰克有许多的想法。
华夏数学界正 于青黄不接的时候。
于青黄不接的时候。
老一辈的数学家都差不多七老八十了,曾经的年轻一代大都在国外任教,新成 起来的一代数学人,目前还没有人有希望摘得菲尔兹奖的殊荣。
起来的一代数学人,目前还没有人有希望摘得菲尔兹奖的殊荣。
目前看来他是最有希望的那一个。
现在世界格局已经很明显,华夏跟 国虽然都有各自的问题,但放
国虽然都有各自的问题,但放 全世界,全已经成了最
全世界,全已经成了最 竞争力的两大势力。
竞争力的两大势力。
ql请记住本站地址http://m.quanbl.com