没有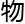
质基础，单凭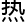
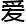，这个行当很难走远。
所以从理论上说，余伟的家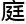
条件还真
适合玩数学的，但乔喻觉得很可惜，毕竟智商不够属于
伤……
可显然余伟并不领
，只在群里发了简短的两个字：“呵呵……”
从这两个字就能看
绪里只有愤怒，没有
恩。
乔喻也开始继续劝解：“我明白你对数学的执念，但你为什么不换个方式呢？比如你老老实实的参加
考，以后上燕北大学的光华学院，然后回家继承亿万家财，运营家族企业。
等你能
钱了，可以投资我以后的研究课题，这样等我了成果也给你加个名字，我们都来
自己最适合的事，这样不但能有成果，还能让你参与度满满。”
蝉不知雪：“乔喻你够了！我承认你暂时比我
，但我肯定会追上你的！不是考试，还是论文！我把话放这里了！”
气势很足，把乔喻都给吓到了，弱弱的在群里问了句：“哦，那你放群里这句话
不到咋办啊？”
余伟半晌没有回话，群里安静了
来。
大概是觉得余伟今天的愤怒值已经满了，小胖
罕见的没在群里继续拱火，而是在乔喻在群里问那句话后，开始跟乔喻私聊起来。
“老大，你也别把余伟打击的太狠了啊！我觉他小宇宙快要爆发了。这样，我正好最近积累了好几
难题，等会让他冷静冷静，你先帮我看看这几题怎么解的。哎，我问老师都还没个我解题方法。规矩我懂，一题五十，转账您收着。”
说着小胖直接给乔喻发了个文档过来，顺手还直接转账了三百块。
看着红灿灿的转账界面，乔喻在心底叹了
气，果然天才都是寂寞的，朋友也无法理解他啊！
直接
了转账面的退回转账，然后说：“你还不明白吗，以后别这样直接发钱了，你攒零
钱也不容易。”
“我靠，谢谢老大！燕北大学果然
，大哥去了之后这格局都不一样了啊！”
“嗯，先别急着谢我，你听过一句话吗？无数普通数学家穷尽一生的努力也不过是帮一个数学天才节省了一个午茶的时间而已。”
“老大，有格局！”
“对，所以我既不会收你的钱，但也不会帮你解题啊。你觉得五十块一题，能
现无数普通数学家穷尽一生努力的价值吗？”
说完，乔喻关了跟余永俊的对话框，切换到了朋友群里，发现余伟还没回话，便主动他，说：“要不这样吧，如果你以后实在追不上我，回家继承家产了就投我的课题咋样？赶
的，我还要研究我的课题呢！”这次余伟到是很快就回话了：“不必了！如果我追不上你，就终生不娶！”
看到余伟这句话，又想到这家伙平日里生冷的
，乔喻突然觉得这玩的有大了，以至于他都顾不上提醒对方，这句话里的歧义让不明真相的人看了，都能脑补n
离经叛的单边故事！
他甚至在脑海
想到了余伟的爹，看到这句话，拿着菜刀朝自己冲过来的样……
毕竟两位大佬级导师主要提供的是学术界
法防御力，理攻击防不住啊！
可见，这家伙是真被气糊涂了！
“别闹，赌这么大，你爹急
了咋办？你家的亿万家财后继无人，不得找我拼命啊！”
“你放一百个心，我有两个哥哥，继承家产这事不差我一个！”
哦，原来还有两个哥哥，难怪敢这么任。
不过乔喻突然想到兰杰那句话，富一代比富二代有意思的多，原来是这么个意思。
毕竟一代的钱自己想怎么就怎么，二代就不一样了，得一代先给了才有得，有两个哥哥的话就更复杂了。
乔喻还在心底叹息着，正打算果断拒绝余伟，毕竟他不喜
男人，余永俊冷不丁的又蹦了来。
“兄弟，以后你需要争家产的时候记得一定要跟我和我大哥说声，我们一定会
定站在你这一边的……另外，老余啊，虽然你的确有几分姿
，但追老大之前，也得先问问老大的取向吧，万一老大是个正常的呢？那个，我截图了啊……”
好吧，看到这句话，乔喻便知接来两个人又要吵起来了，因为他都忍不住把那个胖揍一顿了！
于是果断退微信然后把手机设置成免打扰模式。
还有一周多，这两个家伙就要到燕北大学参加集训了，到时候他自然就能看到余伟会是一副什么表了，但现在让他
疼的还是他给自己找的这个课题。
舒尔茨关于似完备空间理论的五篇论文，他都已经看完了，也消化得差不多了，这段时间还补足了不少基础知识，对于他异想天开的命题，也基本上完成了证明。
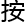照他最初的设想，设x是一个定义在数域k上的维代数曲线，且x是p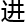
完备代数空间的闭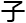集。则存在一个依赖于曲线x的几何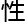质的常数 c，使得曲线上有理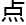的个数满足：n(x)≤c。
这个常数c的确是存在的，乔喻甚至觉得自己的证明过程已经很完
。
而且他也已经求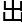了这个常数c的公式。
换句话说，他来燕北大学那天晚上，奇思妙想的命题真的已经被他证明来了。
如果没有那个张教授的话，他说不定已经开始兴致
的写论文了，向数学界公布他的发现！
但现在他还没动笔，因为推这个常数c公式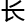
成这样：
最后c1，c2，c3求解之后，
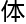的表达式则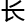成这样：
引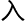
了三个常数a1，a2，a3，分别代表着模形式、-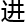同调和量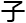化同调范畴相关的常数。而α，β则分别表示与这些几何约束相关的指数，当然亏格g依然是决定上界的主要因素。
没法用，完全没法用。
乔喻尝试着带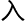到罗伯特教授的工作去，想要利用他的公式去解决一些应用问题，然后很快就发现，确定模形式等级k，质数p的选择，量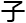化同调参数c的确定，都过于复杂。
公式的常数 a1，a2，a3，以及确定几何结构相关的常数α，β依赖于几何背景跟曲线类型，乔喻实际上手计算的时候，才发现有多麻烦。
这段时间他一直在思考该如何简化公式，让其能变得好用，而且结果依然成立，想了很多
办法，但
碰
。
他已经大概能会到陈师兄的那面对科研大无比的觉了，每次当他想到一办法有可能解决这个问题，然后兴致的冲到电脑前，开始动手解决时，现实都会给他一
。
每次尝试，最后的结果都是此路不通。
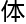
他也专门问过老薛，老薛给他的建议是可以不要寄希望于寻找到一个通用公式，而是直接针对况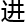行简化，在特定问题削减复杂。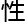
这样在实践也能有一定的应用空间，并能算完全就没有价值。
比如专门针对某一类简单的椭圆曲线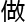一个
ql请记住本站地址http://m.quanbl.com