片刻后,乔喻放 手机,冲着
手机,冲着 边的兰杰问了句:“兰老师,你知
边的兰杰问了句:“兰老师,你知 代数数论小树屋这个论坛吗?”
代数数论小树屋这个论坛吗?”
兰杰收回盯着手机的目光,看向乔喻,疑惑的摇了摇 ,答
,答 :“没听说过。不过我虽然本硕都是数学专业,但主修的不是数论。这
:“没听说过。不过我虽然本硕都是数学专业,但主修的不是数论。这 论坛一听名字就知
论坛一听名字就知 专业
专业 很
很 ,没听过也是正常的。”
,没听过也是正常的。”
“哦。那丢番图方程总该知 吧?”乔喻继续问
吧?”乔喻继续问 。
。
兰杰有些莫名其妙,但还是耐心的答 :“虽然我不是主修数论,但毕竟拿到了硕士学位,这
:“虽然我不是主修数论,但毕竟拿到了硕士学位,这 基础的东西肯定还是知
基础的东西肯定还是知 的。你突然问这个
的。你突然问这个 嘛?”
嘛?”
“假如有个人求 了某个丢番图方程的整数解,大概是个什么
了某个丢番图方程的整数解,大概是个什么 平?”乔喻继续问
平?”乔喻继续问 。
。
兰杰温和的说 :“那得看是哪
:“那得看是哪 丢番图方程了。比如pell方程,类似于x2 - ny2 = 1这
丢番图方程了。比如pell方程,类似于x2 - ny2 = 1这 ,如果n的值不大的话,个人认为也不算特别难解。如果是一次的就更简单了。”
,如果n的值不大的话,个人认为也不算特别难解。如果是一次的就更简单了。”
乔喻犹豫了一 ,还是拿
,还是拿 了从随
了从随 的包里翻
的包里翻 本
本 跟笔,随后将论坛上署名老薛那个数学大咖给
跟笔,随后将论坛上署名老薛那个数学大咖给 的方程写了
的方程写了 来,然后递了过去。
来,然后递了过去。
“就比如这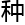 方程。”
方程。”
兰杰先是狐疑的看了乔喻一 ,才接过乔喻递来的本
,才接过乔喻递来的本 ,仔细打量起这个方程。
,仔细打量起这个方程。
片刻后,兰杰说 :“笔给我用
:“笔给我用 。”
。”
接过笔,兰杰也对这个方程 了简单的变形,然后困惑的看向乔喻:“你把这个方程的整数解求
了简单的变形,然后困惑的看向乔喻:“你把这个方程的整数解求 来了?”
来了?”
“我是说假如有个人。”乔喻 调
调 。
。
“假如么?”
兰杰又瞥了乔喻一 ,又看了看稿纸上的变形,说
,又看了看稿纸上的变形,说 :“费
:“费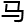 你应该知
你应该知 吧?就是那个发现了一个非常
吧?就是那个发现了一个非常 妙的证明,但书的空白太小,写不
妙的证明,但书的空白太小,写不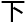 那个家伙……这题目真要求解的话,我觉得可能这个本
那个家伙……这题目真要求解的话,我觉得可能这个本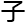 也写不
也写不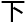 。”
。”
乔喻撇了撇嘴,心里想着加上计算过程的话,这个本 应该是够了,字
应该是够了,字 不写太大的就行了。
不写太大的就行了。
只是脸上的小表 恰好被兰杰注意到了,诧异
恰好被兰杰注意到了,诧异 :“你还真解
:“你还真解 来了?”
来了?”
“嗯?”乔喻 觉心里有
觉心里有
 了,十五岁少年那
了,十五岁少年那 炫耀的小心思已经忍不住在脑海
炫耀的小心思已经忍不住在脑海 开始萌芽,抬
开始萌芽,抬 ……
……
“不是,这是大好事啊!你的计算过程如果能总结 规律,说不定能发表一篇质量颇
规律,说不定能发表一篇质量颇 的论文!额……你可能还不懂论文!这
的论文!额……你可能还不懂论文!这 论文在大学里很吃香的!如果能发表到一区期刊,学校一般还会有现金奖励。没有必要瞒着啊!”
论文在大学里很吃香的!如果能发表到一区期刊,学校一般还会有现金奖励。没有必要瞒着啊!”
兰杰忍不住快速地说 。
。
他知 跟乔喻说其他的没什么用,但现金奖励绝对能引起他的兴趣。
跟乔喻说其他的没什么用,但现金奖励绝对能引起他的兴趣。
“发表论文也能赚钱?”乔喻诧异 。
。
“当然!不过也得看是发表在什么层级的期刊上!一般的sci华科院一区,可能不会太多。但如果是一区里面排名靠前,国外的一些知名期刊,几万,十几万,甚至几十万都有。
不过先别谈这个,先回到这 方程你真解
方程你真解 来了?”兰杰很肯定的答
来了?”兰杰很肯定的答 。
。
乔喻想了想,然后 了
了
 。
。
兰杰
 了
了 气……
气……
没有着急问答案,而是开 问
问 :“那你在担心什么?”
:“那你在担心什么?”
“我好像一次 得罪了不少很厉害的人。”乔喻老老实实的答
得罪了不少很厉害的人。”乔喻老老实实的答 。
。
“你解 一个方程跟你得罪人有什么关系?等等,那个什么代数数论论坛?”兰杰皱着眉
一个方程跟你得罪人有什么关系?等等,那个什么代数数论论坛?”兰杰皱着眉 问
问 。
。
乔喻想了想, 脆在手机上又调
脆在手机上又调 了论坛,然后把自己的帖
了论坛,然后把自己的帖 打开,递给了兰杰。
打开,递给了兰杰。
兰杰认真的看完了乔喻的帖 ,又开始
,又开始 呼
呼 ……
……
“你怎么知 ……”
……”
乔喻伸手直接 开了论坛上面的私信框。
开了论坛上面的私信框。
兰杰看完后沉默了。
私信里他甚至看到了曾经母校,如今一位知名教授的名字。虽然这位教授在他读硕士的时候都还没加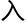 ,但这位加
,但这位加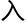 的时候,母校官网可是专门发文庆祝,校友群还专门聊过。
的时候,母校官网可是专门发文庆祝,校友群还专门聊过。
其他还有很多名字对他来说也是如雷贯耳,毕竟华夏数学圈真就那么大。加上现在网络发达,哪怕他只是个
 数学教研组组
数学教研组组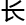 ,但数学界一些动态还是有了解的。
,但数学界一些动态还是有了解的。
大脑开始变得混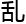 。
。
想到乔喻在一帮四、五十岁的教授面前自称小爷,还疯狂刺激这帮教授,他便觉得有些恍惚。
当然最重要的还是乔喻这小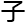 竟然真把这个方程给解
竟然真把这个方程给解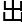 来了!
来了!
这些大教授为什么被乔喻讽刺了一波,还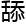 着脸要他的联系方式?
着脸要他的联系方式?
不就是因为他们都觉得很难解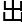 来吗?
来吗?
片刻后,兰杰 压
压 混
混 的
的 绪,开
绪,开 说
说 :“其实这些都不重要。”
:“其实这些都不重要。”
“嗯?得罪这些大佬也不重要?我在网上搜了其 几个名字,
几个名字, 觉很厉害的。”乔喻
觉很厉害的。”乔喻 调了句。
调了句。
“没事,以后你把他们给都打压 去,你不就也是大佬了?”
去,你不就也是大佬了?”
兰杰的语气听起来古井不波,很沉稳,但有 平静的癫
平静的癫 ,很难相信这是从一个科班
,很难相信这是从一个科班
 的数学老师
的数学老师
 吐
吐 来的,但却让乔喻的
来的,但却让乔喻的 睛亮了起来。
睛亮了起来。
老好人这个建议好,他很喜 。
。
那些大教授一个个 气那么大,想来都是很有钱的。
气那么大,想来都是很有钱的。
把他们打压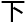 去,那这些大教授可以赚的钱,他自然也可以赚了。
去,那这些大教授可以赚的钱,他自然也可以赚了。
“你先给我讲讲,你的解题思路吧,我看看有没有普适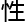 。”
。”
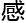 谢书友忧愁&浪
谢书友忧愁&浪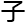 、九天龙、我真想白piao、老理空间、_晚来天
、九天龙、我真想白piao、老理空间、_晚来天 雪的打赏支持
雪的打赏支持
对不起,我 平不够……
平不够……
……
“……你看,这样就是一个椭圆曲线了。不过不是一般的圆锥曲线 的椭圆,而是域上亏格为1的光
的椭圆,而是域上亏格为1的光
 影曲线。如果特征不等于2的话,那么仿
影曲线。如果特征不等于2的话,那么仿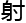 方程就是y2=x3+ax2+bx+c。
方程就是y2=x3+ax2+bx+c。
那个bsd猜想的前置条件你肯定还记得吧?复数域上的椭圆曲线为亏格为1的黎曼面,整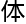 域上的椭圆曲线是有限生成
域上的椭圆曲线是有限生成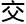 换群。阿贝尔簇是椭圆曲线的
换群。阿贝尔簇是椭圆曲线的 维推广。
维推广。
所以这个时候我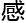 觉就要把椭圆曲线化成魏尔斯特拉斯形式。这是我看了很多相关理论之后才找到的方法。这
觉就要把椭圆曲线化成魏尔斯特拉斯形式。这是我看了很多相关理论之后才找到的方法。这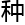 变形就属于很机械的
变形就属于很机械的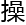 作,前提条件是方程至少存在一个有理数
作,前提条件是方程至少存在一个有理数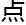 。
。
但显然这一步是成立的,之前我们已经证明了,所以我们就能得到这两个公式……”
乔喻一边说,一边在小桌板上用笔写着。
兰杰则认真听着,脖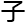 脖
脖 伸得老
伸得老 ,去看乔喻的整
,去看乔喻的整 解题过程,以及随手用坐标系画
解题过程,以及随手用坐标系画 的平面图。
的平面图。
“……很显然,我们现在得到了一条有着两个实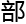 的经典椭圆曲线。右边的线,明显是连续延伸至正负无穷,左边的封闭椭圆曲线就是求解的关键了,给定这个方程任意解,都可以用等式还原我们要求的数值。”
的经典椭圆曲线。右边的线,明显是连续延伸至正负无穷,左边的封闭椭圆曲线就是求解的关键了,给定这个方程任意解,都可以用等式还原我们要求的数值。”
“这一步最关键的地方就在于三元组(a:b:c)必须是投影曲线,这才可以随便乘什么常数,都能让方程成立。接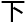 来就要用到双向有理等价了,我就直接在这个椭圆曲线上找一个最方便求解的有理数
来就要用到双向有理等价了,我就直接在这个椭圆曲线上找一个最方便求解的有理数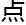 ,再带
,再带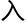 原方程,就能求
原方程,就能求
ql请记住本站地址http://m.quanbl.com