但好在他的选择够果断。
安装完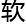 件当天就提
件当天就提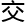 了辞职报告,第二天就雷厉风行的从谷歌离职,这些天还
了辞职报告,第二天就雷厉风行的从谷歌离职,这些天还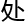 理大
理大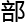 分的
分的 票,然后分散到多个账
票,然后分散到多个账 之
之 。
。
兰利的专业人员判断的没错,伊森·威廉姆斯的确想办法 了两
了两
 份。
份。
在辞职第二天,他先是用原本的 份飞到了边境的佛州,然后用新
份飞到了边境的佛州,然后用新 份买了辆二手车直接到了邻国,并在邻国直接飞到了夏威夷。手段很
份买了辆二手车直接到了邻国,并在邻国直接飞到了夏威夷。手段很 糙,但在
糙,但在 急
急 况
况 ,这已经是他能想到最稳妥的办法了。
,这已经是他能想到最稳妥的办法了。
其实他依然要 谢豆豆,为了让这家伙逃的更顺利,豆豆也是在网络跟通信上
谢豆豆,为了让这家伙逃的更顺利,豆豆也是在网络跟通信上 了力的。这大概率不是善良,而是背锅侠必须要显得很专业。
了力的。这大概率不是善良,而是背锅侠必须要显得很专业。
在不违背任何法律的同时,要 到这些,其实还真是
到这些,其实还真是 吃力的……
吃力的……
……
华夏,西林工大。
大学校园像是一座金字塔能把外面那些魑魅魍魉有效的拦截在校门之外。让众多涉世未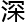 的孩
的孩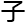 们能保证成年后最后一段纯真。尤其是乔班的孩
们能保证成年后最后一段纯真。尤其是乔班的孩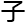 们。
们。
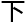 午两
午两 ,小课堂上,许昌树准时走
,小课堂上,许昌树准时走 了教室。
了教室。
这得 谢徐大江的
谢徐大江的 作,让数研所的教授们都要参与到乔班的教学工作,许昌树自然也不例外。
作,让数研所的教授们都要参与到乔班的教学工作,许昌树自然也不例外。
不过跟其他教授不同,许昌树对此并不抗拒。
他当初申请调到西林工大时,本就是教职。当时本想是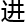 数学院的,恰逢西林数研所成立,便
数学院的,恰逢西林数研所成立,便 脆直接
脆直接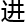 了数研所。
了数研所。
现在他则是乔班《代数几何》代数簇的任课教授。
在数学院这是大三才会接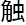 的课程,不过乔班的这门课程教科书是新编纂的,参考了gt211的
的课程,不过乔班的这门课程教科书是新编纂的,参考了gt211的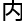 容,同时加
容,同时加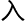 了一些乔代数几何基础。
了一些乔代数几何基础。
不过关于乔代数几何基础的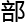 分在
分在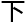 册
册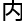 容
容 ,要第三学期才会正式接
,要第三学期才会正式接 ,教科书还没发到学生手上。
,教科书还没发到学生手上。
乔班已经正式开课两周了,这门课程每周安排了四节课, 度很
度很 。
。
但许昌树能 觉到最近这些不知
觉到最近这些不知 天
天 地厚的小家伙们有些浮躁了。
地厚的小家伙们有些浮躁了。
从平日的作业就能看 来。
来。
 分同学玩的很
分同学玩的很 。比如已经在作业里给教授留思考题了……
。比如已经在作业里给教授留思考题了……
所以今天许昌树决定给这些所谓的小天才们上一课……
说起来,谁在这么大的时候还不是老师
 的天才了?
的天才了?
当代表上课的音乐声停 ,许昌树没有像往常一样打开教案,而是直接开始在黑板上板书。
,许昌树没有像往常一样打开教案,而是直接开始在黑板上板书。
很快几个名词就已经在黑板上被书写 来。
来。
虚界数ξ:在乔代数 ,它代表
,它代表 维的转换。
维的转换。
旋元素w:乔空间的基本旋转,可以被看作是一个引导超螺旋结构变换的 心元素。
心元素。
跃迁数t:乔代数 ,跃迁数代表从一个维度到另一个维度的
,跃迁数代表从一个维度到另一个维度的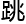 跃,用于描述不同维度间的相互作用和连接。
跃,用于描述不同维度间的相互作用和连接。
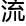 形因
形因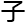 μ:乔空间
μ:乔空间 用来衡量和调控形态复杂度的参数,影响着空间的形态和扩展。
用来衡量和调控形态复杂度的参数,影响着空间的形态和扩展。
将这四个基本概念写完之后,许昌树转过 ,看向讲台
,看向讲台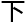 一脸懵
一脸懵 的孩
的孩 们。
们。
“你们 有人觉得我们目前课程
有人觉得我们目前课程 度太慢了,完全是浪费时间,所以想要接
度太慢了,完全是浪费时间,所以想要接 些新的东西,所以我决定满足你们。今天我们提前接
些新的东西,所以我决定满足你们。今天我们提前接 一
一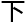 乔代数几何
乔代数几何 的
的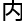 容。板书上这四个最基本的特殊数,就是乔代数最基础的概念。
容。板书上这四个最基本的特殊数,就是乔代数最基础的概念。
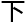 午的两堂课这样安排,第一堂课我会先讲解几个例题,让你们尝试理解这些概念,以及它们的数学属
午的两堂课这样安排,第一堂课我会先讲解几个例题,让你们尝试理解这些概念,以及它们的数学属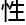 和应用。第二堂课我会布置两
和应用。第二堂课我会布置两 乔代数
乔代数 针对这四个概念最简单的题目,你们有一堂课的时间来解答。
针对这四个概念最简单的题目,你们有一堂课的时间来解答。
如果你们能顺利完成,我会重新修改教案,让你们提前接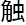 新的
新的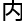 容。当然,如果没人能答得
容。当然,如果没人能答得 来,那我建议你们还是老老实实的
来,那我建议你们还是老老实实的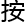 照我的既定教案来。有问题吗?”
照我的既定教案来。有问题吗?”
“没问题!”十个人声音洪亮气氛昂扬的回答 。
。
之所以十二个人的课堂上,只有十个人回答,主要是有两个人 本不敢吱声……
本不敢吱声……
是的,此时的顾正梁跟张舟都已经被震撼到了。
就正常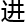 度都特么已经很难了,每天作业要写到大半夜,还玩
度都特么已经很难了,每天作业要写到大半夜,还玩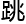 跃?这特么谁啊!这个班能不能多两个正常人?
跃?这特么谁啊!这个班能不能多两个正常人?
可惜,这两个人的反应被许昌树完全无视了。
这位资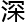 的燕北教授,曾经也是小学六年级就已经掌握了微积分的天才微微一笑,然后开始写起了例题。
的燕北教授,曾经也是小学六年级就已经掌握了微积分的天才微微一笑,然后开始写起了例题。
假设在一个多维超螺旋空间 ,存在一
,存在一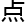 p在虚界数ξ的作用
p在虚界数ξ的作用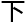 通过旋元素w
通过旋元素w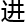 行了一个基本的旋转变换。现在考虑使用跃迁数t将
行了一个基本的旋转变换。现在考虑使用跃迁数t将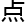 p从其原始位置跃迁到新位置 q。
p从其原始位置跃迁到新位置 q。
已知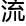 形因
形因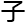 μ表示从p到q的空间曲率和拓扑变化。
μ表示从p到q的空间曲率和拓扑变化。
1、给定 p的初始坐标为(x,y,z),ξ作用于 p后的坐标变为(?y,x,z)。应用w=eiθ(其 θ为给定的旋转角度),求
θ为给定的旋转角度),求 p的新坐标。
p的新坐标。
2、如果t是一个描述由p到q的跃迁映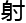 ,且μ表示这
,且μ表示这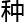 变换
变换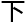 的空间变化率,请描述在μ的影响
的空间变化率,请描述在μ的影响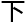 ,t如何改变 p到q的路径。
,t如何改变 p到q的路径。
台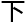 前所未有的安静,写完例题后,许昌树转
前所未有的安静,写完例题后,许昌树转 ,看向这些专注的孩
,看向这些专注的孩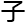 ,笑了笑,然后开始讲解:“首先,让我们看第一个问题,这是一
,笑了笑,然后开始讲解:“首先,让我们看第一个问题,这是一 简单的计算题,但要求解,首先我们要理解题
简单的计算题,但要求解,首先我们要理解题 的表述。
的表述。
参考我刚才写的基本概念,p在ξ的作用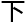 通过w
通过w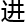 行一个基本旋转变换,大家首先想到了什么?”
行一个基本旋转变换,大家首先想到了什么?”
台 很安静,片刻后有人说
很安静,片刻后有人说 :“旋转矩阵?”
:“旋转矩阵?”
“对,旋转矩阵,但并不全对,因为你只考虑了旋转,没有考虑到维度的变化,因为ξ本 还代表着
还代表着 维的转换,所以你们要这样理解……”
维的转换,所以你们要这样理解……”
朝气蓬 的少年们
的少年们
张舟跟顾正梁互相看了 。都能从各自的
。都能从各自的 神
神 看
看 那
那 无辜……
无辜……
这特么都是什么玩意儿?不用听了,真的。
太过 象的
象的 容,如果对于代数几何的前置不够了解,听不懂的。
容,如果对于代数几何的前置不够了解,听不懂的。
恰好两人对于自己的知识储备有着还算清晰的认知。
他们的同学的确有人早早接 过gt211,甚至gt52的
过gt211,甚至gt52的 容,但他们真没接
容,但他们真没接 过。
过。
典型的爬都还没学会,大人就想教他们跑了。
毕竟 维的转换,汉字看起来非常简单,都是常用字,但如果数学语言来表述……
维的转换,汉字看起来非常简单,都是常用字,但如果数学语言来表述……
“什么是 维的转换?其实很简单,你们如果暂时没有一个直观的理解,可以先把ξ视为一个微分算
维的转换?其实很简单,你们如果暂时没有一个直观的理解,可以先把ξ视为一个微分算 ,例如在一个光
,例如在一个光 的
的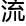 形上,ξ可以被定义为一个旋量场,其在局
形上,ξ可以被定义为一个旋量场,其在局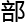 坐标系
坐标系 的表示涉及到clifford代数的元素,这些元素是用于描述空间
的表示涉及到clifford代数的元素,这些元素是用于描述空间 的旋转和反
的旋转和反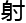 的代数结构。
的代数结构。
那么它的数学表示就是这个形式……”
许昌树再次转 板书,并给
板书,并给 了答案。
了答案。
“大家应该看懂了吧,那么让我们回到原题 ……”
……”
……
张舟跟顾正梁已经彻底放弃了,这已经不是错过一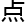 就看不懂了,这是从开
就看不懂了,这是从开 就看不懂。
就看不懂。
ql请记住本站地址http://m.quanbl.com