约翰继续 :“你父亲的算法,的确已经是人类最杰
:“你父亲的算法,的确已经是人类最杰 的作品,但还远远不够
的作品,但还远远不够 大。所以,我们没有办法将
大。所以,我们没有办法将 聚变装置
聚变装置 的更小,每一个反应炉都像一座座山岳一样,简直太
的更小,每一个反应炉都像一座座山岳一样,简直太 暴了。”
暴了。”
张远看着这些湍 ,有的明亮,有的黯淡,还有的正在旋转,陷
,有的明亮,有的黯淡,还有的正在旋转,陷 了沉思。
了沉思。
不 服不服气,约翰的抱怨的确没错。
服不服气,约翰的抱怨的确没错。
他心 产生了一
产生了一 小小的野心,就好像
小小的野心,就好像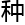
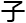 一样生
一样生 发芽。
发芽。
“曾经父亲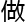 过的问题,或许……我也能?!”
过的问题,或许……我也能?!”
湍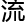 问题,经典
问题,经典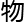 理学
理学 最后一座大山。大约在400年前,纳维-斯托克斯方程,也即n-s方程,就已对
最后一座大山。大约在400年前,纳维-斯托克斯方程,也即n-s方程,就已对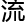
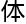 的
的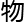 理
理 行了理论的描述。这一方程一般很难求
行了理论的描述。这一方程一般很难求
 确解,所以科学家通常采用一些简化的理论模型或者求助于数值模拟的方法来预测
确解,所以科学家通常采用一些简化的理论模型或者求助于数值模拟的方法来预测
 的运动。
的运动。
但用简化模型来模拟等离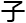 湍
湍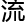 ,实在太不
,实在太不 确。如果这些等离
确。如果这些等离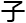 没有约束好,会对聚变引擎造成
没有约束好,会对聚变引擎造成 大的破坏。
大的破坏。
信息学的蓬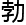 发展,让湍
发展,让湍 问题
问题 现了一些松动,但也仅仅只是一些松动,能够模拟地更加准确,却不能
现了一些松动,但也仅仅只是一些松动,能够模拟地更加准确,却不能
 了解其真正本质。
了解其真正本质。
约翰叹息 :“我们可能永远找不到湍
:“我们可能永远找不到湍 问题在数学上的
问题在数学上的 确解,或许说完全的
确解,或许说完全的 确隐藏在更加微观的概率叠加态当
确隐藏在更加微观的概率叠加态当 ,以我们的能力,完全不知
,以我们的能力,完全不知 。”
。”
约翰?维尔逊是悲观派的典型代表。
他认为,人类科技的上限很可能已经是目前这样了,以人类的智商,只能在这么一丁 圈
圈 里转来转去。
里转来转去。
虽然还有一些细枝末节的东西有待打磨,但总归不可能真正地实现质变。
所以,这群悲观派的科学家想要登上飞船,想要看看三千年以后的世界。
这个说法不是没有 理,一个湍
理,一个湍 问题,
问题, 了四百年的时间都没有彻底解决。
了四百年的时间都没有彻底解决。
尖端 理学
理学 ,除了凝聚态还保持旺盛的活力外,其他的都已经渐渐消沉。
,除了凝聚态还保持旺盛的活力外,其他的都已经渐渐消沉。 能
能 理被“能级大沙漠”困扰,其他的学科,譬如化学、半导
理被“能级大沙漠”困扰,其他的学科,譬如化学、半导 ,使用的竟然是一些近似理论,最关键的是,这些近似理论确实能够解决一些问题。
,使用的竟然是一些近似理论,最关键的是,这些近似理论确实能够解决一些问题。
至于数学方面,也正在慢慢走 坡路。
坡路。
黎曼猜想,400年屹立不倒;哥德 赫猜想,600年了。
赫猜想,600年了。
“数学大统一”计划到现在还只是一个框架,距离完成还有几百亿光年的距离。
新文明学派认为,现在的23世纪,再加上24、25世纪,很可能是人类最后的黄金盛世。再接 来,人类的整
来,人类的整 智力无法继续发展
智力无法继续发展 去。
去。
一旦科技停滞发展,人类文明很可能如同古代夏国那样,不停地发生历史 回的现象。用学术一
回的现象。用学术一 的词语,也就是掉
的词语,也就是掉 “平庸化的陷阱”当
“平庸化的陷阱”当 ,很难再取得历史
,很难再取得历史 的
的 大
大 步。
步。
张远其实 同意新文明学派的
同意新文明学派的 分观
分观 ,但对于这个问题,他既不悲观也不乐观。
,但对于这个问题,他既不悲观也不乐观。
他其实不太相信,人类会蠢到掉 可以预见的陷阱当
可以预见的陷阱当 ,也很难想象未来的世界究竟怎么样,说不定会
,也很难想象未来的世界究竟怎么样,说不定会 现一些改造智力的科技呢。
现一些改造智力的科技呢。
再加上他从事的方向比较偏向于工科,偏向技术。技术与科学还是有很大的不同的,人类的应用技术提升,确实还有很大的空间。
“张,你太乐观了。”
约翰耸了耸肩膀,无可奈何地说 :“在历史
:“在历史 ,有很多现象,譬如说拉
,有很多现象,譬如说拉 化,
化, 等国家收
等国家收 陷阱等等。就算某些国家明明知
陷阱等等。就算某些国家明明知 ,却依旧无法跨越,因为一个国家的许多事
,却依旧无法跨越,因为一个国家的许多事 ,不是领导人意识到了就能够
,不是领导人意识到了就能够 到的。得依靠整
到的。得依靠整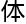 的力量。”
的力量。”
“但人类的集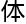 力量,并不像你想象
力量,并不像你想象 的那样
的那样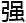 大。”
大。”
“是啊,你说的很对。”张远 :“不过我们总得保持乐观,不是吗?悲观也不可能解决什么问题。”
:“不过我们总得保持乐观,不是吗?悲观也不可能解决什么问题。”
告别了这位多愁善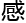 的约翰师兄,张远回到自己的实验室座位,开始继续翻阅文献。
的约翰师兄,张远回到自己的实验室座位,开始继续翻阅文献。
无意间翻到一本书。
《十万个未解之谜》……
从天文到地理,从数学到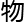 理,没办法解开的难题实在太多了。譬如说“3x+1”猜想、
理,没办法解开的难题实在太多了。譬如说“3x+1”猜想、 好结局问题、
好结局问题、 斯圆问题、erdos-graha 三
斯圆问题、erdos-graha 三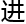 制问题……随随便便一个,难度都堪比黎猜。
制问题……随随便便一个,难度都堪比黎猜。
不知 为什么,看着无数的难题,张远心
为什么,看着无数的难题,张远心 总是有一
总是有一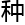 微微的恼怒
微微的恼怒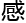 。
。
或许,是作为科研工作者 的一员,无法彻底
的一员,无法彻底 穿自然的本能恼怒。
穿自然的本能恼怒。
张远暗地里 了
了 拳
拳 。
。
在这一刹那,他终于 定决心,去解决一个世界知名难题。
定决心,去解决一个世界知名难题。
无所谓得与失,只是遵循自己的本心罢了。
“湍 问题!”
问题!”
“试一试吧!”
这需要很大的勇气。
很可能 了很多很多的时间,什么成果都
了很多很多的时间,什么成果都 不
不 ,沉没成本
,沉没成本 大。也就只有他这
大。也就只有他这 年轻人,凭着一腔
年轻人,凭着一腔 血,就能够勇往直前。
血,就能够勇往直前。
 定决心后,张远
定决心后,张远
 吐了一
吐了一 气,慢慢地沉
气,慢慢地沉 心思。
心思。
从纯数学的角度,基本上没什么太大的可能。
张远不觉得自己目前的实力,能够写 比n-s方程更加
比n-s方程更加 确有效的方程式。
确有效的方程式。
“或许,可以创造一些信息学的方法,来解决这个问题。”
第一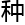 方法,是父亲所用的,大名鼎鼎的“小波变换的谱方法”,也是目前工程应用
方法,是父亲所用的,大名鼎鼎的“小波变换的谱方法”,也是目前工程应用 最好的算法。它成功解决了引擎
最好的算法。它成功解决了引擎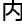
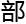
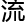 动在时间和空间都为多尺度的湍
动在时间和空间都为多尺度的湍 模拟问题。
模拟问题。
本质上,是借鉴了信号在神经元 的传递过程,来描述
的传递过程,来描述

 湍
湍 的猝发机制。
的猝发机制。
第二 方法,是直接数值求解的方法。
方法,是直接数值求解的方法。
通过解不可压缩
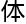 的“n-s方程”对在三维周期立方
的“n-s方程”对在三维周期立方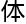
 的各项同
的各项同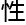 的湍
的湍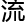
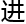 行模拟。不过,这
行模拟。不过,这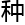 方法对算力的要求很
方法对算力的要求很 ,适用于计算雷诺数较低的简单湍
,适用于计算雷诺数较低的简单湍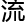 运动,例如槽
运动,例如槽 或圆
或圆 湍
湍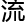 。
。
当然还有第三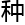 “rngk-e模型”、第四
“rngk-e模型”、第四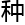 “spart—allaras湍
“spart—allaras湍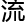 模型”、第五
模型”、第五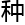 方法“
方法“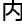 外迭代法”等等。
外迭代法”等等。
人的创造力是无限的,不过真正有意义、有应用价值的算法总归只有这么几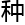 。
。
“你在看湍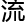 问题?这玩意不是一般的复杂!”
问题?这玩意不是一般的复杂!”
赵青锋瞥了他的屏幕一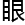 ,饶有兴趣地说
,饶有兴趣地说 :“我曾经也研究过这方面的
:“我曾经也研究过这方面的 容,
容, 心原因是问题本
心原因是问题本 难度过大,
难度过大, 非线
非线 、无限维系统、混沌系统,这三个难
、无限维系统、混沌系统,这三个难 目前都没有非常适合的数学工
目前都没有非常适合的数学工 。”
。”
“所以你想 的话,我也没有特别好的建议给你。”
的话,我也没有特别好的建议给你。”
“我知 ,就是随便看看。”张远连忙
,就是随便看看。”张远连忙 。
。
赵师兄笑了一 ,
, 慨着年轻真好,如果是他本人,肯定会离这
慨着年轻真好,如果是他本人,肯定会离这 问题远远的。
问题远远的。
不过他并没有在意太多,有很多东西,只要了解过了,就会知难而退。
ql请记住本站地址http://m.quanbl.com